题目内容
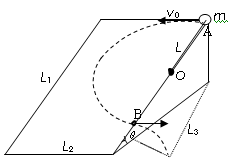
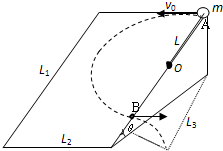
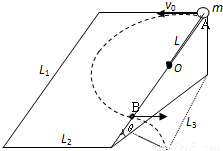
如图所示，一个长L1＝0.9m、宽L2＝0.6m的光滑斜面体，其倾角θ＝30°.有一长度L＝0.4m的轻质绳一端固定在距斜面顶点Ａ为L＝0.4m斜面边缘的Ｏ点上，另一端系一质量m=1kg的小球.现把小球拉至顶点Ａ处，以v0＝2m/s的初速度沿斜面顶边缘水平抛出.（g取10m/s2）
（1）刚开始小球做什么运动？并说明理由.
（2）求小球运动至斜面边缘Ｂ点时受到绳子的拉力ＦT.
（3）若小球运动至Ｂ点时绳子刚好断了，求小球从斜面上飞出后落地点与最初抛出点在地面上投影点的距离L3.(最后结果可用根式表示)
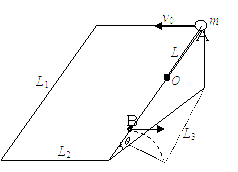
（1）（2）(3)
（1）因为刚抛出的速度v0=2m/s＞vmin，故小球从开始就做圆周运动
（2）ＦＴ=35Ｎ
（3）
解析:
⑴设小球沿斜面向下的重力的分力为：
此力产生的加速度
代入数据得：a=5m/s2 （2分）
其在斜面上运动可等效看作在g′=a＝5m/s2的竖直平面上的曲线运动，
由于小球在最高点做圆周运动的最小速度是恰好由重力沿斜面的分力提供向心力，
由牛顿第二定律得：
（2分） ，
（1分）
因为刚抛出的速度v0=2m/s＞vmin，故小球从开始就做圆周运动（1分）
(2)如图所示，当它运动在最低点时，设速度为v1, 由于只有重力做功，所以机械能守恒，
所以 
① （2分）
② （1分）
代入数据解得：
（1分）
或者由动能定理得：
代入数据解得：
在最低点，根据牛顿第二定律有：
（2分）
代入数据解得：ＦＴ=35Ｎ （1分）
(3)绳断后小球以v1做平抛运动，由题中已知可得小球下落的高度h′=0.05m，设至落地所需时间为t′,
根据
解得：t′＝0.1s （2分）
平抛的水平位移x＝v1 t′＝0.1
m （2分）
而斜面直径在地面投影有效长度为Ｌ４＝0.4
m （1分）
所求的距离
（2分）
阅读快车系列答案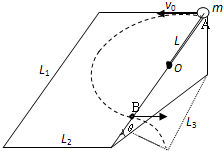
如图所示，一个长L1=0.9m、宽L2=0.6m的光滑斜面体，其倾角θ=30°．有一长度L=0.4m的轻质绳一端固定在距斜面顶点A为L=0.4m斜面边缘的O点上，另一端系一质量m=1kg的小球．现把小球拉至顶点A处，以v0=1m/s的初速度沿斜面顶边缘水平抛出．（g取10m/s2）
