题目内容
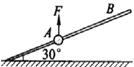
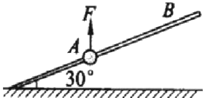如图所示，一质量为1kg的小球套在一根固定的直杆上，直杆与水平面夹角θ为30°．现小球在F=20N的竖直向上的拉力作用下，从A点静止出发向上运动，已知杆与球间的动摩擦因数μ=
| ||
| 6 |
（1）小球运动的加速度a1；
（2）若F作用1.2s后撤去，小球上滑过程中距A点最大距离sm．
分析：首先分析撤去前小球的受力情况：重力、拉力，杆的支持力和滑动摩擦力，采用正交分解法，根据牛顿第二定律求出加速度．再用同样的方法求出撤去后小球的加速度，运用运动学公式求出最大距离．
解答：解：（1）在力F作用时有：
（F-mg）sin30°-m（F-mg）cos30°=ma1
a1=2.5 m/s2
（2）刚撤去F时，小球的速度v1=a1t1=3m/s
小球的位移s1 =
t1=1.8m
撤去力F后，小球上滑时有：
mgsin30°+μmgcos30°=ma2
a2=7.5 m/s2
因此小球上滑时间t2=
=0.4s 上滑位移s2=
t2=0.6m
则小球上滑的最大距离为sm=s1+s2=2.4m
答：（1）小球运动的加速度为2.5 m/s2 ；
（2）若F作用1.2s后撤去，小球上滑过程中距A点最大距离为2.4m．
（F-mg）sin30°-m（F-mg）cos30°=ma1
a1=2.5 m/s2
（2）刚撤去F时，小球的速度v1=a1t1=3m/s
小球的位移s1 =
| v1 |
| 2 |
撤去力F后，小球上滑时有：
mgsin30°+μmgcos30°=ma2
a2=7.5 m/s2
因此小球上滑时间t2=
| v1 |
| a2 |
| v1 |
| 2 |
则小球上滑的最大距离为sm=s1+s2=2.4m
答：（1）小球运动的加速度为2.5 m/s2 ；
（2）若F作用1.2s后撤去，小球上滑过程中距A点最大距离为2.4m．
点评：牛顿定律和运动学公式是解决力学的基本方法．关键在于分析物体的受力情况和运动情况．当物体受力较多时，往往采用正交分解法求加速度．本题求小球上滑过程中距A点最大距离，也可运用动能定理．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
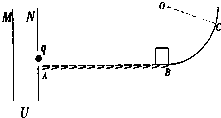如图所示，一质量为1×10-4kg，带电量为5×10-6C的带电粒子在一加速电压为1×105V的电场中，从静止开始加速，飞出电场后水平击中静止在光滑圆弧底端的小木块，并随小木块一起以5m/s的速度向前滑行，已知水平轨道AB=10m，与木块的动摩擦因素μ=0.5，BC是半径R=300m的光滑圆弧轨道．试求：
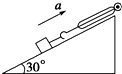已知一些材料间的动摩擦因数如下表所示：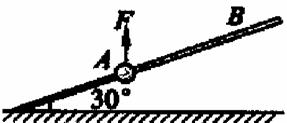
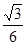。试求：
。试求：（1）小球运动的加速度a1；（2）若F作用1．2s后撤去，小球上滑过程中距A点最大距离sm；（3）若从撤去力F开始计时，小球经多长时间将经过距A点上方为2．25 m的B点。
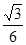。试求：