题目内容
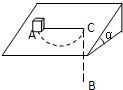 在一个与水平面成α角的粗糙斜面上的A点放着一个物体,它系于一根不可伸长的细绳上,绳子的另一端B通过小孔C穿出底面,如图所示,开始时物体与C等高,当物体开始缓慢下滑时,适当的拉动绳端B,使物体在斜面上划过一个半圆到达C,则A和斜面之间的动摩擦因数μ为
在一个与水平面成α角的粗糙斜面上的A点放着一个物体,它系于一根不可伸长的细绳上,绳子的另一端B通过小孔C穿出底面,如图所示,开始时物体与C等高,当物体开始缓慢下滑时,适当的拉动绳端B,使物体在斜面上划过一个半圆到达C,则A和斜面之间的动摩擦因数μ为
- A.sinα
- B.cosα
- C.tanα
- D.cotα
C
分析:物体缓慢转动,近似平衡,受力分析后,根据平衡条件列式求解.
解答:物体在斜面上缓慢运动时,受到4个力:重力G,绳子的拉力F1,斜面的支持力F2,物体在运动时受到的摩擦力F3,这四个力的合力近似为零;
其中F1和F3同斜面平行,F2同斜面垂直,G同斜面成(90°-α).
根据各力之间的平衡的原则,可列出以下公式:
在垂直斜面方向,有:F2=G?cos α
因此有摩擦力F3=μ F2=μGcosα
接下来考虑平行于斜面的力,为了简化问题状态,可以直接以A点处的系统状态来进行分析,此时时摩擦力和重力在斜面平行方向上的力是反向、等大的,即应该是近似平衡的,有
μGcosα=Gsinα
因此 μ=tan α
故选C.
点评:这个解法最有技巧的部分就是选取了A点处受力分析,根据平衡条件得到重力的下滑分量等于摩擦力,然后列式求解;当然,也可以对其它点处,运用平衡条件列式.
分析:物体缓慢转动,近似平衡,受力分析后,根据平衡条件列式求解.
解答:物体在斜面上缓慢运动时,受到4个力:重力G,绳子的拉力F1,斜面的支持力F2,物体在运动时受到的摩擦力F3,这四个力的合力近似为零;
其中F1和F3同斜面平行,F2同斜面垂直,G同斜面成(90°-α).
根据各力之间的平衡的原则,可列出以下公式:
在垂直斜面方向,有:F2=G?cos α
因此有摩擦力F3=μ F2=μGcosα
接下来考虑平行于斜面的力,为了简化问题状态,可以直接以A点处的系统状态来进行分析,此时时摩擦力和重力在斜面平行方向上的力是反向、等大的,即应该是近似平衡的,有
μGcosα=Gsinα
因此 μ=tan α
故选C.
点评:这个解法最有技巧的部分就是选取了A点处受力分析,根据平衡条件得到重力的下滑分量等于摩擦力,然后列式求解;当然,也可以对其它点处,运用平衡条件列式.

练习册系列答案
相关题目
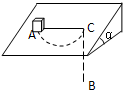 在一个与水平面成α角的粗糙斜面上的A点放着一个物体,它系于一根不可伸长的细绳上,绳子的另一端B通过小孔C穿出底面,如图所示,开始时物体与C等高,当物体开始缓慢下滑时,适当的拉动绳端B,使物体在斜面上划过一个半圆到达C,则A和斜面之间的动摩擦因数μ为( )
在一个与水平面成α角的粗糙斜面上的A点放着一个物体,它系于一根不可伸长的细绳上,绳子的另一端B通过小孔C穿出底面,如图所示,开始时物体与C等高,当物体开始缓慢下滑时,适当的拉动绳端B,使物体在斜面上划过一个半圆到达C,则A和斜面之间的动摩擦因数μ为( )