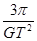题目内容
一艘宇宙飞船贴近一恒星表面飞行,测得它匀速圆周运动的周期为T,设万有引力常数G,则此恒星的平均密度为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据万有引力提供向心力求出恒星的质量,结合体积求出恒星的平均密度.
解答:解:设恒星的半径为R,根据万有引力提供向心力得,
G
=mR
,
解得恒星的质量M=
.
则恒星的密度ρ=
=
=
.故B正确,A、C、D错误.
故选:B.
G
| Mm |
| R2 |
| 4π2 |
| T2 |
解得恒星的质量M=
| 4π2R3 |
| GT2 |
则恒星的密度ρ=
| M |
| V |
| ||
|
| 3π |
| GT2 |
故选:B.
点评:解决本题的关键掌握万有引力提供向心力这一理论,并能灵活运用,注意飞船贴近星球表面飞行,则轨道半径等于恒星的半径.

练习册系列答案
相关题目
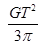
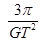
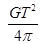
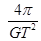
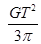 B.
B.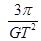 C.
C.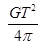 D.
D.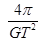
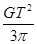 B.
B.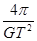 C.
C.
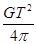 D.
D.