题目内容
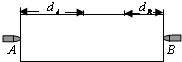 如图所示,木块静止在光滑的水平面上,子弹A、B从木块两侧同时水平射入木块,最终都停在木块中,这一过程中木块始终保持静止.现知道子弹A射入的深度dA大于子弹B射入的深度dB.用tA、tB表示它们在木块中的运动时间,用EkA、EkB表示它们的初动能,用vA、vB表示它们的初速度大小,用mA、mB表示它们的质量,则可判断( )
如图所示,木块静止在光滑的水平面上,子弹A、B从木块两侧同时水平射入木块,最终都停在木块中,这一过程中木块始终保持静止.现知道子弹A射入的深度dA大于子弹B射入的深度dB.用tA、tB表示它们在木块中的运动时间,用EkA、EkB表示它们的初动能,用vA、vB表示它们的初速度大小,用mA、mB表示它们的质量,则可判断( )| A、tA>tB | B、EkA>EkB | C、vA>vB | D、mA>mB |
分析:根据子弹A、B从木块两侧同时射入木块,木块始终保持静止,分析子弹在木块中运动时间的关系.根据动能定理研究初动能的关系.根据动量守恒定律研究质量关系.
解答:解:A、由题,子弹A、B从木块两侧同时射入木块,木块始终保持静止,分析得知,两子弹在木块中运动时间必定相等,否则木块就会运动.故A错误.
B、由于木块始终保持静止状态,则两子弹对木块的推力大小相等,则两子弹所受的阻力大小相等,设为f,根据动能定理得:
对A子弹:-fdA=0-EkA,得EkA=fdA
对B子弹:-fdB=0-EkB,得EkB=fdB.
由于dA>dB,则有子弹入射时的初动能EkA>EkB.故B正确.
CD、对两子弹和木块组成的系统动量守恒,因动量与动能的关系为:P=
,则有:
=
,而EkA>EkB,则得到mA<mB.
根据动能的计算公式Ek=
mv2,得到初速度vA>vB.故C正确,D错误.
故选:BC.
B、由于木块始终保持静止状态,则两子弹对木块的推力大小相等,则两子弹所受的阻力大小相等,设为f,根据动能定理得:
对A子弹:-fdA=0-EkA,得EkA=fdA
对B子弹:-fdB=0-EkB,得EkB=fdB.
由于dA>dB,则有子弹入射时的初动能EkA>EkB.故B正确.
CD、对两子弹和木块组成的系统动量守恒,因动量与动能的关系为:P=
| 2mEk |
| 2mAEKA |
| 2mBEkB |
根据动能的计算公式Ek=
| 1 |
| 2 |
故选:BC.
点评:本题运用动能定理和动量守恒定律研究冲击块模型,分析木块处于静止状态,确定出两子弹所受的阻力大小相等是基础.

练习册系列答案
相关题目
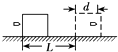 如图所示,木块静止在光滑水平桌面上,一子弹水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿桌面移动的距离为L,木块对子弹的平均阻力为f,那么在这一过程中( )
如图所示,木块静止在光滑水平桌面上,一子弹水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿桌面移动的距离为L,木块对子弹的平均阻力为f,那么在这一过程中( ) 如图所示,木块静止在固定斜面上,关于木块的受力情况,以下说法正确的是( )
如图所示,木块静止在固定斜面上,关于木块的受力情况,以下说法正确的是( ) (2006?上海模拟)如图所示,木块静止在光滑水平面上,子弹A、B从木块两侧同时射入木块,最终都停在木块中,这一过程中木块始终保持静止.现知道子弹A射入深度dA大于子弹B射入的深度dB,则可判断( )
(2006?上海模拟)如图所示,木块静止在光滑水平面上,子弹A、B从木块两侧同时射入木块,最终都停在木块中,这一过程中木块始终保持静止.现知道子弹A射入深度dA大于子弹B射入的深度dB,则可判断( )