题目内容
10.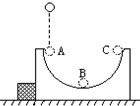 如图所示将一半径为R、质量为M的光滑半圆槽置于光滑水平面上,槽的左侧有一固定在水平面上的物块,今让一质量为m的小球自左侧槽口A的正上方距槽口A高为h的位置从静止开始落下,与圆弧槽相切自A点进入槽内,试求:
如图所示将一半径为R、质量为M的光滑半圆槽置于光滑水平面上,槽的左侧有一固定在水平面上的物块,今让一质量为m的小球自左侧槽口A的正上方距槽口A高为h的位置从静止开始落下,与圆弧槽相切自A点进入槽内,试求:(1)小球运动到图中B位置时速度为多大?
(2)小球从位置C离开时,半圆槽的速度是多大?
(3)小球离开C后,还能上升多大的高度.
分析 (1)根据动能定理研究小球自离槽口到B点,求出球到达B点速度,
(2)当小球在半圆槽内运动的B到C过程中,槽也会向右运动.水平方向满足动量守恒.当球到达A点即将与槽分离时,小球和槽具有相同的水平方向速度,小球与槽组成的系统机械能守恒.
(3)球离开槽后向上做斜上抛运动,当竖直方向的分速度等于0时,上升的高度最大.
解答 解:(1)根据动能定理研究小球自离槽口到B点,
mg(h+R)=$\frac{1}{2}$m${v}_{B}^{2}$
vB=$\sqrt{2(h+R)}$,
(2)当小球在半圆槽内运动的B到C过程中,槽也会向右运动.水平方向满足动量守恒.当球到达A点即将与槽分离时,小球和槽具有相同的水平方向速度,规定向右为正方向,根据水平方向系统动量守恒得
mvB=(M+m)v
得:v=$\frac{m\sqrt{2(h+R)}}{M+m}$,方向水平向右.
(3)球离开槽后向上做斜上抛运动,当竖直方向的分速度等于0时,上升的高度最大,此时小球与槽具有相等的水平速度,根据小球与槽组成的系统机械能守恒得:
$\frac{1}{2}$m${v}_{B}^{2}$=mg(R+H)+$\frac{1}{2}$Mv2+$\frac{1}{2}$mv2
整理得:H=$h-\frac{m(h+R)}{M+m}$
答:(1)小球运动到图中B位置时速度为$\sqrt{2(h+R)}$;
(2)小球从位置C离开时,半圆槽的速度是$\frac{m\sqrt{2(h+R)}}{M+m}$;
(3)小球离开C后,还能上升的高度是$h-\frac{m(h+R)}{M+m}$.
点评 考查动量守恒定律与机械能守恒定律.当球下落到最低点过程,由于左侧竖直墙壁作用,小球与槽组成的系统水平方向上的动量不守恒,但小球机械能守恒.当球从最低点上升时,小球与槽组成的系统水平方向上的动量守恒.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | 某高速公路上的限速为110 km/h,指的是瞬时速度 | |
| B. | 汽车速度计上显示80 km/h,指的是平均速度 | |
| C. | 火车从济南到北京的速度约为220 km/h,指的是瞬时速度 | |
| D. | 子弹以900 km/h的速度从枪口射出,指的是瞬时速度 |
| A. | 受力大小为零 | |
| B. | 受力大小为$\frac{kqQ}{{R}^{2}}$,方向由圆孔指向球心 | |
| C. | 受力大小为$\frac{kqQ{r}^{2}}{4{R}^{4}}$,方向由圆孔指向球心 | |
| D. | 受力大小为$\frac{kqQ{r}^{2}}{4{R}^{4}}$,方向由球心指向圆孔 |
| A. | 速度 | B. | 加速度 | C. | 合外力 | D. | 角速度 |

| A. | 从A点运动到B点过程中,“嫦娥二号”受到月球的引力增大 | |
| B. | 从A点运动到B点过程中,月球对“嫦娥二号”的引力做负功 | |
| C. | “嫦娥二号”在A点比在B点的速度小 | |
| D. | “嫦娥二号”在A点比在B点的速度大 |
| A. | 物体带电一定指带有多余的电子 | |
| B. | 物体所带电荷量可能是1.5e | |
| C. | 只有摩擦才能使物体带电 | |
| D. | 摩擦起电实质是电子从一个物体转移到另一个物体 |
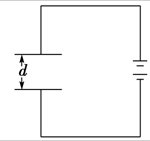 将电容C=3.0×10-10F,两极板间距离d=1.20×10-3m的平行板电容器始终接在电压为10V的直流电源上.如图所示,取g=10m/s2.
将电容C=3.0×10-10F,两极板间距离d=1.20×10-3m的平行板电容器始终接在电压为10V的直流电源上.如图所示,取g=10m/s2.