题目内容
14.如图是将演示简谐振动图象的装置作变更,当盛砂漏斗下面的薄木板被匀加速地拉出时,摆动着的漏斗中漏出的砂在木板上形成的曲线如图示,A、B、C、D、E均为OO′轴上的点,AB=S1,BC=S2,摆长为L(可视作不变)摆角小于5°,则木板的加速度为多大?(已知当地的重力加速度为g)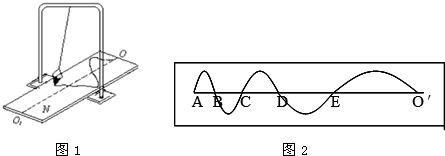
分析 漏斗做简谐运动,具有周期性;木板做匀加速直线运动;根据沙在木板上显示的曲线,A到C或C到E的时间等于沙摆的周期,AB、BC时间为$\frac{T}{2}$,板做匀加速运动,由公式T=2π$\sqrt{\frac{L}{g}}$和△s=aT2求加速度.
解答 解:根据公式△s=aT2,有:
${S}_{2}-{S}_{1}=a(\frac{T}{2})^{2}$ ①
单摆的摆长为L,做简谐运动,周期为T=2π$\sqrt{\frac{L}{g}}$ ②
①②联立解得:$a=\frac{{({S_2}-{S_1})g}}{{{π^2}L}}$
答:木板的加速度为$a=\frac{{({S_2}-{S_1})g}}{{{π^2}L}}$.
点评 本题关键明确单摆的摆动和木板的运动具有等时性,然后结合匀变速直线运动的推论公式△s=aT2和单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$列式求解即可.

练习册系列答案
相关题目
4.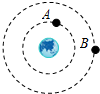 2015年3月30日,我国成功发射第一颗北斗全球组网试验星,经过多次变轨,先后在低空A轨道和高空B轨道绕地球做圆周运动,如图所示.则改“试验星”在A轨道运行时( )
2015年3月30日,我国成功发射第一颗北斗全球组网试验星,经过多次变轨,先后在低空A轨道和高空B轨道绕地球做圆周运动,如图所示.则改“试验星”在A轨道运行时( )
 2015年3月30日,我国成功发射第一颗北斗全球组网试验星,经过多次变轨,先后在低空A轨道和高空B轨道绕地球做圆周运动,如图所示.则改“试验星”在A轨道运行时( )
2015年3月30日,我国成功发射第一颗北斗全球组网试验星,经过多次变轨,先后在低空A轨道和高空B轨道绕地球做圆周运动,如图所示.则改“试验星”在A轨道运行时( )| A. | 线速度大于7.9km/s | B. | 线速度比在B轨道的大 | ||
| C. | 周期比在B轨道的长 | D. | 所需向心力比在B轨道的大 |
5. 如图所示,质量为m的小球用长为L的悬线固定于O点,在O点正下方O′处钉一个钉子,把悬线拉直与竖直方向成一定角度,由静止释放小球,当悬线碰到钉子时,则( )
如图所示,质量为m的小球用长为L的悬线固定于O点,在O点正下方O′处钉一个钉子,把悬线拉直与竖直方向成一定角度,由静止释放小球,当悬线碰到钉子时,则( )
 如图所示,质量为m的小球用长为L的悬线固定于O点,在O点正下方O′处钉一个钉子,把悬线拉直与竖直方向成一定角度,由静止释放小球,当悬线碰到钉子时,则( )
如图所示,质量为m的小球用长为L的悬线固定于O点,在O点正下方O′处钉一个钉子,把悬线拉直与竖直方向成一定角度,由静止释放小球,当悬线碰到钉子时,则( )| A. | 小球的线速度v突然变大 | B. | 小球的向心加速度a突然变小 | ||
| C. | 小球的角速度ω突然变小 | D. | 悬线的张力突然变大 |
9.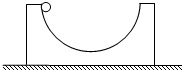 如图所示,一质量为M的光滑半圆形凹槽静止放在光滑水平面上,凹槽的半径为R,另一质量为m(M=2m)的小球(可视为质点)从凹槽的左侧最高点由静止释放,从开始到小球滑至凹槽最低点的过程中,下列说法中正确的是( )
如图所示,一质量为M的光滑半圆形凹槽静止放在光滑水平面上,凹槽的半径为R,另一质量为m(M=2m)的小球(可视为质点)从凹槽的左侧最高点由静止释放,从开始到小球滑至凹槽最低点的过程中,下列说法中正确的是( )
 如图所示,一质量为M的光滑半圆形凹槽静止放在光滑水平面上,凹槽的半径为R,另一质量为m(M=2m)的小球(可视为质点)从凹槽的左侧最高点由静止释放,从开始到小球滑至凹槽最低点的过程中,下列说法中正确的是( )
如图所示,一质量为M的光滑半圆形凹槽静止放在光滑水平面上,凹槽的半径为R,另一质量为m(M=2m)的小球(可视为质点)从凹槽的左侧最高点由静止释放,从开始到小球滑至凹槽最低点的过程中,下列说法中正确的是( )| A. | 小球与凹槽组成的系统动量守恒 | |
| B. | 小球与凹槽组成的系统机械能不守恒 | |
| C. | 小球动量的改变量等于其重力的冲量 | |
| D. | 凹槽向左移动的距离为$\frac{1}{3}$R |
19.下列说法正确的是( )
| A. | 静摩擦力对物体一定做正功 | |
| B. | 滑动摩擦力对物体一定做正功 | |
| C. | 若物体下落时,重力一定做正功 | |
| D. | 若作用力做正功,则反作用力一定做负功 |
3.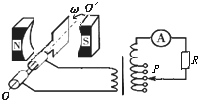 如图,有一面积为S,匝数为N的矩形线圈绕OO′轴在磁感强度为B的匀强磁场中以角速度ω匀速转动.从图示位置开始计时,下列判断正确的是( )
如图,有一面积为S,匝数为N的矩形线圈绕OO′轴在磁感强度为B的匀强磁场中以角速度ω匀速转动.从图示位置开始计时,下列判断正确的是( )
 如图,有一面积为S,匝数为N的矩形线圈绕OO′轴在磁感强度为B的匀强磁场中以角速度ω匀速转动.从图示位置开始计时,下列判断正确的是( )
如图,有一面积为S,匝数为N的矩形线圈绕OO′轴在磁感强度为B的匀强磁场中以角速度ω匀速转动.从图示位置开始计时,下列判断正确的是( )| A. | 电流表测的是最大值 | |
| B. | 感应电动势的瞬时值表达式为e=NBSω•sinωt | |
| C. | P向上移动时,电流表示数变大 | |
| D. | P向上移动时,电流表示数变小 |
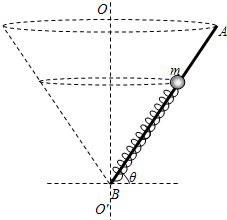 如图所示,光滑杆AB长2m,B端固定一根劲度系数为k=40N/m、原长为l0=1m的轻弹簧,质量为m=0.2kg的小球套在光滑杆上并与弹簧的上端连接.OO′为过B点的竖直轴,杆与水平面间的夹角始终为θ=53°.g取10m/s2
如图所示,光滑杆AB长2m,B端固定一根劲度系数为k=40N/m、原长为l0=1m的轻弹簧,质量为m=0.2kg的小球套在光滑杆上并与弹簧的上端连接.OO′为过B点的竖直轴,杆与水平面间的夹角始终为θ=53°.g取10m/s2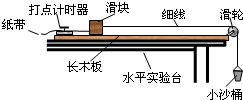 某探究学习小组的同学欲验证动能定理,他们在实验室组装了一套如图所示的装置,另外他们还准备了导线、小木块、细沙等.若你是小组中的一位成员,要完成该项实验:
某探究学习小组的同学欲验证动能定理,他们在实验室组装了一套如图所示的装置,另外他们还准备了导线、小木块、细沙等.若你是小组中的一位成员,要完成该项实验: