��Ŀ����
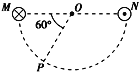
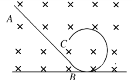
����Ŀ����ͼ��ʾ��ABCΪ��ֱƽ���ڵĹ⻬��Ե���������ABΪ��бֱ�����BCΪ��AB���е�Բ�ι��������װ�ô�����ǿ�ų��У��ų�����ֱֽ�����������ͬ�Ŀɿ����ʵ�ļס�������С�����硢��������硣�ֽ�����С���ڹ��AB�Ϸֱ����ͬ�߶ȴ��ɾ�ֹ�ͷţ�����ͨ��Բ�ι����ߵ㣬���� ��
A. ������ߵ�ʱ��������ٶȱ�����С
B. ������ߵ�ʱ������С����ٶ����
C. ���������ǡ��ͨ����ߵ��������ͷ�λ�ñ�����ĸ�
D. ����С����͵�ʱ�Թ����ѹ����С��ͬ
���𰸡�B
��������
���������������������������ϵ��֪��������ߵ�ʱ��������ٶȵ���������ٶȣ�����ţ�ٵڶ������ж����������ǡ��ͨ����ߵ�ʱ������ٶȹ�ϵ�����ж������ͷ�λ�ù�ϵ������ţ�ٵڶ�������ʽ�Ƚ�����С����͵�ʱ�Թ����ѹ����С.
���������ͬ�ĸ߶�A����ʼ�ͷŵ�С��Բ����ߵ�����У���������������ȣ���������������������ߵ�ʱ��������ٶȵ���������ٶȣ�ѡ��A����B��ȷ������ǡ�ܾ�����ߵ�ʱ��mg=m![]() ������mg+qv��B=m
������mg+qv��B=m![]() ����v��>v������֪������ͷ�λ�ñ�����ĵͣ�ѡ��C��������С����͵�ʱ���ٶ���ͬ������͵㣬�Լ���
����v��>v������֪������ͷ�λ�ñ�����ĵͣ�ѡ��C��������С����͵�ʱ���ٶ���ͬ������͵㣬�Լ���![]() ��������
��������![]() ����֪N��>N����ѡ��D����ѡB.
����֪N��>N����ѡ��D����ѡB.

 ��У����ϵ�д�
��У����ϵ�д�