题目内容
16. 如图所示,水平放置的平行板电容器的极板长L=0.4m,两板间距离d=4×10-3m;在电容器两板不带电的情况下,有一束带电粒子,以相同的速率v0从两板中央沿平行极板方向水平射入两板之间,粒子流恰好落在下板的正中央;已知每个带电粒子的质量m=4×10-5kg,电量q=+1×10-8C.重力加速度g=10m/s2.为使粒子流能从平行板电容器的右侧射出电场,求:
如图所示,水平放置的平行板电容器的极板长L=0.4m,两板间距离d=4×10-3m;在电容器两板不带电的情况下,有一束带电粒子,以相同的速率v0从两板中央沿平行极板方向水平射入两板之间,粒子流恰好落在下板的正中央;已知每个带电粒子的质量m=4×10-5kg,电量q=+1×10-8C.重力加速度g=10m/s2.为使粒子流能从平行板电容器的右侧射出电场,求:(1)电容器的上板应与电源的正极还是负极相连?
(2)所加的电压U的大小.
分析 粒子刚进入平行板时,两极板不带电,粒子做的是平抛运动,根据平抛运动的规律可以求得粒子入射速度v0的大小;由于两板之间加入了匀强电场,此时带电粒子在电场中的运动是类平抛运动,仍把运动在水平和竖直两个方向上分解,进行列式计算.由于带电粒子的水平位移增加,在板间的运动时间变大,而竖直方向位移不变,所以在竖直方向的加速度减小了,由此可判断受到了竖直向上的电场力作用,再结合牛顿运动定律列式求解即可.
解答 解:(1)粒子刚进入平行板时,两极板不带电,粒子做的是平抛运动,则有:
水平方向有:$\frac{L}{2}={v}_{0}t$
竖直方向有:$\frac{d}{2}=\frac{1}{2}g{t}^{2}$
解得:v0=10m/s
由于带电粒子的水平位移增加,在板间的运动时间变大,而竖直方向位移不变,所以在竖直方向的加速度减小,所以电场力方向向上,又因为是正电荷,所以上极板与电源的负极相连,
(2)当所加电压为U1时,微粒恰好从下板的右边缘射出,则有:
$\frac{d}{2}=\frac{1}{2}{a}_{1}(\frac{L}{{v}_{0}})^{2}$
根据牛顿第二定律得mg-$q\frac{{U}_{1}}{d}$=ma1,
解得:U1=120V
当所加电压为U2时,微粒恰好从上板的右边缘射出,则有:$\frac{d}{2}=\frac{1}{2}{a}_{2}(\frac{L}{{v}_{0}})^{2}$
根据牛顿第二定律得:$q\frac{{U}_{2}}{d}-mg=m{a}_{2}$,
解得:U2=200V
所以所加电压的范围为:120V<U<200V.
答:(1)上极板与电源的负极相连.
(2)所加电压的范围为120V<U<200V.
点评 解得此类问题,首先要正确的对带电粒子在这两种情况下进行正确的受力分析,确定粒子的运动类型.解决带电粒子垂直射入电场的类型的题,应用平抛运动的规律进行求解.
此类型的题要注意是否要考虑带电粒子的重力,原则是:除有说明或暗示外,对基本粒子(例如电子,质子、α粒子、离子等),一般不考虑重力;对带点微粒,(如液滴、油滴、小球、尘埃等),一般要考虑重力.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案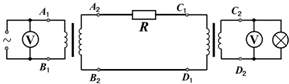 远程输电的原理图如图所示,升压变压器和降压变压器都可看作理想变压器,有关说法正确的是( )
远程输电的原理图如图所示,升压变压器和降压变压器都可看作理想变压器,有关说法正确的是( )| A. | 升压变压器原线圈的输入功率与降压变压器的输出功率相等 | |
| B. | 升压变压器副线圈两端的电压与降压变压器原线圈的电压相等 | |
| C. | 升压变压器副线圈的电流与降压变压器原线圈的电流相等 | |
| D. | 由P=$\frac{{U}^{2}}{R}$得,输电线损失的功率与输电电压的平方成正比 |
| A. | 法拉第通过油滴实验测定了元电荷的数值 | |
| B. | 牛顿利用开普勒第三定律和牛顿第三定律发现了万有引力定律 | |
| C. | 库仑通过自己大量的实验研究发现了静止的点电荷之间的相互作用规律 | |
| D. | 伽利略利用斜面实验推翻了亚里士多德的“力是维持物体运动的原因”的观点 |
 如图甲所示是一打桩机的简易模型,质量m=1kg的重锤在拉力F作用下从与钉子接触处由静止开始竖直向上运动,上升一段高度后撤去F,重锤自由上升到最高点后再自由下落,撞击钉子,将钉子打入一定深度.重锤上升过程中,其机械能E与上升高度h的关系图象如图所示,不计空气阻力,不计重锤跟竖直滑竿之间的摩擦,g取10m/s2,则( )
如图甲所示是一打桩机的简易模型,质量m=1kg的重锤在拉力F作用下从与钉子接触处由静止开始竖直向上运动,上升一段高度后撤去F,重锤自由上升到最高点后再自由下落,撞击钉子,将钉子打入一定深度.重锤上升过程中,其机械能E与上升高度h的关系图象如图所示,不计空气阻力,不计重锤跟竖直滑竿之间的摩擦,g取10m/s2,则( )| A. | 重锤受到的拉力F大小为12N | |
| B. | 重锤上升到1.0m处的速度为4m/s | |
| C. | 撤去F后物体上升的总时间为0.1s | |
| D. | 重锤上升到0.25m高度处时拉力F的为12W功率 |
 如图所示,一轻弹簧竖直放置,下端固定在水平面上,上端处于a位置,当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置,现将重球(视为质点)从高于a位置的c位置沿弹簧中轴线自由下落,弹簧被重球压缩到最低位置d.以下关于重球运动过程的正确说法应是( )
如图所示,一轻弹簧竖直放置,下端固定在水平面上,上端处于a位置,当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置,现将重球(视为质点)从高于a位置的c位置沿弹簧中轴线自由下落,弹簧被重球压缩到最低位置d.以下关于重球运动过程的正确说法应是( )| A. | 重球下落压缩弹簧由a至d的过程中,重球做减速运动 | |
| B. | 重球由a至b的过程中,小球的动能和机械能均增加 | |
| C. | 重球在b位置处具有的动能等于小球由c下落到b处减少的重力势能 | |
| D. | 由a到d过程中重球克服弹簧弹力做的功等于小球由c下落到d处时重力势能减少量 |
| A. | 光子说的确立完全否定了波动说 | |
| B. | 光的波粒二象性是指光既与宏观概念中的波相同又与微观概念中的粒子相同 | |
| C. | 光的波动说和粒子说都有其正确性,但又都是不完善的,都有其不能解释的实验现象 | |
| D. | 光的波粒二象性才是对光的本性的正确认识 |
| A. | 质量 | B. | 力 | C. | 位移 | D. | 速度 |
 如图所示,一列简谐横波沿x轴正方向传播着,振幅为2cm.t=0时刻平衡位置坐标分别为40m、100m的P、Q两质点的位移均为1cm,质点P的速度方向沿y轴负方向,质点Q与之相反.已知P、Q两质点间只有一个波峰,则
如图所示,一列简谐横波沿x轴正方向传播着,振幅为2cm.t=0时刻平衡位置坐标分别为40m、100m的P、Q两质点的位移均为1cm,质点P的速度方向沿y轴负方向,质点Q与之相反.已知P、Q两质点间只有一个波峰,则