题目内容
9.甲、乙两车在两条平行车道上沿直线向同一方向行驶,某时刻乙在前,甲在后,相距80m,该时刻甲车的速度为36km/h,乙车的速度为108km/h,甲做加速度为5m/s2的匀加速直线运动,乙立刻刹车做加速度为15m/s2的匀减速直线运动,则:(1)经过多少时间甲、乙两车在相遇前相距最远?
(2)在相遇前甲、乙两车相距的最远距离是多少?
((3)经过多长时间甲、乙两车相遇?
分析 (1)当两者速度相同时相距最远,根据速度时间公式求的时间,结合位移时间公式求的相距最远的距离;
(2)判断出乙减速到零甲是否追上乙,如果没追上,乙停止后不动,甲继续做匀加速运动,根据位移时间公式求的追上的时间
解答 解:(1)v甲=36km/h=10m/s,v乙=108km/h=30m/s
速度相同时两车相距最远
即v=v甲+a甲t=v乙+a乙t
解得t=1s,v=15m/s
(2)在1s内甲前进的位移为${x}_{甲}={v}_{甲}t+\frac{1}{2}{a}_{甲}{t}^{2}=10×1+\frac{1}{2}×5×{1}^{2}$m=12.5m
乙前进的位移为${x}_{乙}=\frac{{v}_{乙}+v}{2}t=\frac{30+15}{2}×1m=22.5m$
相距距离为△X=△x+x乙-x甲=80+22.5-12.5m=90m
(3)乙减速到零所需时间为$t′=\frac{0-{v}_{乙}}{{a}_{乙}}=2s$
2s内乙前进的位移为$x′=\frac{{v}_{乙}+0}{2}t′=30m$
甲前进的位移为$x″={v}_{甲}t′+\frac{1}{2}{a}_{甲}t{′}^{2}$=30m
此时两者相距距离为△x′=△x+x′-x″=80m,未相遇
故相遇时甲的位移为x总=△x+x′=110m
${x}_{总}={v}_{甲}{t}_{总}+\frac{1}{2}{{a}_{甲}t}_{总}^{2}$
解得t=$4\sqrt{3}-2$s
答:(1)经过1s甲、乙两车在相遇前相距最远
(2)在相遇前甲、乙两车相距的最远距离是90m
(3)经过$4\sqrt{3}-2$s时间甲、乙两车相遇
点评 本题考查了求甲追上 乙需要的时间,分析清楚物体的运动过程、应用匀变速直线运动规律即可正确解题

| A. | 并联用电器增多,电路的总电阻增大 | |
| B. | 并联用电器增多,电路的总电流减小 | |
| C. | 并联用电器增多,家用电器的实际功率减小 | |
| D. | 并联用电器增多,家用电器的额定功率减小 |
| A. | 当两个带电体的形状对它们间相互作用力的影响可忽略时,这两个带电体可看作点电荷 | |
| B. | 只有体积很小的带电体才可能看作点电荷 | |
| C. | 体积较大的带电体一定不是点电荷 | |
| D. | 点电荷并非理想模型,而是真实存在的 |
| A. | 伽利略研究自由落体运动时,遇到的困难是无法准确测量下落时间和瞬时速度 | |
| B. | 无风的房间中将一根柔软的羽毛由静止释放,羽毛将做自由落体运动 | |
| C. | 自由落体运动就是初速度为0,加速度a=g的匀加速直线运动 | |
| D. | 自由落体物体前三个连续相等时间间隔的位移比为1:3:5 |
 为了最大限度地减少道路交通事故,全省各地开始了“集中整治酒后驾驶违法行为”专项行动.这是因为一般驾驶员酒后的反应时间(从发现情况到开始制动所需的时间)比正常时慢了0.1~0.5s,易发生交通事故.
为了最大限度地减少道路交通事故,全省各地开始了“集中整治酒后驾驶违法行为”专项行动.这是因为一般驾驶员酒后的反应时间(从发现情况到开始制动所需的时间)比正常时慢了0.1~0.5s,易发生交通事故.| 车速v(km/h) | 40 | 60 | 80 |
| 反应距离s(m) | 5 | 7.5 | 10 |
(2)如图所示,假设一饮酒后的驾驶员驾车以54km/h的速度在平直公路上行驶,在距离某学校门前25m处发现有一队学生在斑马线上横过马路,他的反应时间比正常时慢了0.5s,刹车后,车做加速度大小为7.5m/s2的匀减速直线运动.试通过计算说明是否会发生交通事故.
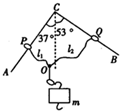 如图所示,ACB是一光滑的、足够长的、固定在竖直平面内的“∧”形框架,其中CA、CB两边足够长且与竖直方向的夹角分别为37°和53°,P、Q两个轻质小环分别套在CA、CB上,两根细绳l1、l2的一端分别系在P、Q环上,另一端和一绳套系在一起,结点为O.l1能承受的最大张力为10N,l2能承受的最大张力为5N,绳套能承受很大的拉力.现将质量为50g的钩码一个一个地串在绳套下面,O点最多能挂多少个这样的钩码?(g取10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,ACB是一光滑的、足够长的、固定在竖直平面内的“∧”形框架,其中CA、CB两边足够长且与竖直方向的夹角分别为37°和53°,P、Q两个轻质小环分别套在CA、CB上,两根细绳l1、l2的一端分别系在P、Q环上,另一端和一绳套系在一起,结点为O.l1能承受的最大张力为10N,l2能承受的最大张力为5N,绳套能承受很大的拉力.现将质量为50g的钩码一个一个地串在绳套下面,O点最多能挂多少个这样的钩码?(g取10m/s2,sin37°=0.6,cos37°=0.8)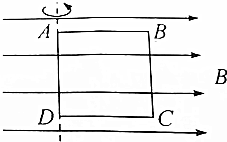 如图所示,边长为0.1m、共20匝的正方形线圈ABCD在磁感应强度为0.5T的匀强磁场中以AD边为轴匀速转动.初始时刻线圈平面与磁感线平行,经过0.1s线圈转了90°,求:
如图所示,边长为0.1m、共20匝的正方形线圈ABCD在磁感应强度为0.5T的匀强磁场中以AD边为轴匀速转动.初始时刻线圈平面与磁感线平行,经过0.1s线圈转了90°,求: