Question

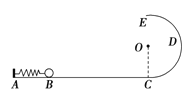
【题目】如图所示，半径为R的光滑半圆形轨道CDE在竖直平面内与光滑水平轨道AC相切于C点，水平轨道AC上有一轻质弹簧，弹簧左端连接在固定的挡板上，弹簧自由端B与轨道最低点C的距离为4R，现用一个小球压缩弹簧（不拴接），当弹簧的压缩量为l时，释放小球，小球在运动过程中恰好通过半圆形轨道的最高点E；之后再次从B点用该小球压缩弹簧，释放后小球经过BCDE轨道抛出后恰好落在B点，已知弹簧压缩时弹性势能与压缩量的二次方成正比，弹簧始终处在弹性限度内，求第二次压缩时弹簧的压缩量。

Answer 1

【答案】

【解析】

试题分析：设第一次压缩量为时，弹簧的弹性势能为。

释放小球后弹簧的弹性势能转化为小球的动能，设小球离开弹簧时速度为v1

由机械能守恒定律得

设小球在最高点E时的速度为v2，由临界条件可知，解得

由机械能守恒定律可得

以上几式联立解得

设第二次压缩时弹簧的压缩量为x，此时弹簧的弹性势能为

小球通过最高点E时的速度为v3，由机械能守恒定律可得

小球从E点开始做平抛运动，由平抛运动规律得

解得，解得

由已知条件可得，代入数据解得。