题目内容
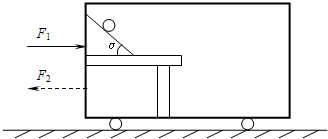如图所示，车厢内的小桌上固定一光滑斜面，除去小球车厢的总质量为M、小球的质量为m，斜面倾角为α．车在水平推力作用下向右做匀加速直线运动，小球（视为质点）始终与车相对静止，小球距桌面的高度为h，距车厢地板高度为H，离桌面边缘水平距离为L，离车厢前壁的距离为d．车在运动过程中所受的阻力等于车对地面压力的k倍，重力加速度为g．
（1）、求水平推力F1的大小
（2）、若M=10kg，m=1kg，α=37°，k=0.20，h=0.20m，H=0.80m，L=0.30m，d=1.60m，g=10m/s2．当车速为v0=15m/s时，撤去推力F1同时对车施加水平向左的拉力F2（如虚线所示），小球立即离开斜面向右飞去．为使小球在运动中不碰到桌子和前壁，所加拉力F2应满足什么条件？
解：（1）对小球进行受力分析，根据牛顿第二定律得：
mgtanα=ma
解得a=gtanα
对整体有：
F1-k（M+m）=（M+m）a
解得：F1=（M+m）g（k+tanα）
（2）撤去推力F1同时对车施加水平向左的拉力F2（如虚线所示），小球立即离开斜面向右飞去．
此时小球做平抛运动，为使小球在运动中不碰到桌子和前壁，则小球刚好运动到桌子右端或车厢右下角．
若小球刚好运动到桌子右端，则
运动的时间为；t=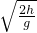
=
水平位移为：x=v0t=3m
所以车厢运动的位移为s=x-L=2.7m
对车厢有：s=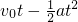
解得：a=15m/s2
F2+kMg=Ma
解得F2=130N
若小球刚好运动到车厢右下角，则
运动的时间为；t=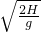
=
水平位移为：x=v0t=6m
所以车厢运动的位移为s=x-d=4.4m
对车厢有：s=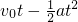
解得：a=20m/s2
F2+kMg=Ma
解得F2=180N
综上可知：为使小球在运动中不碰到桌子和前壁，所加拉力F2应满足130N＜F2＜180N．
答：（1）、求水平推力F1的大小为（M+m）g（k+tanα）；
（2）、为使小球在运动中不碰到桌子和前壁，所加拉力F2应满足130N＜F2＜180N．
分析：（1）对小球进行受力分析，根据牛顿第二定律求得加速度，对整体根据牛顿第二定律即可求解F1的大小；
（2）撤去推力F1同时对车施加水平向左的拉力F2（如虚线所示），小球立即离开斜面向右飞去．此时小球做平抛运动，为使小球在运动中不碰到桌子和前壁，则小球刚好运动到桌子右端或车厢右下角．车厢在F2的作用下做匀减速运动，根据位移关系求出加速度，再根据牛顿第二定律即可求解．
点评：本题主要运用了隔离法和整体法，要根据题目需要选择研究对象运用牛顿第二定律求解，要注意小球离开斜面后做平抛运动，难度较大．
mgtanα=ma
解得a=gtanα
对整体有：
F1-k（M+m）=（M+m）a
解得：F1=（M+m）g（k+tanα）
（2）撤去推力F1同时对车施加水平向左的拉力F2（如虚线所示），小球立即离开斜面向右飞去．
此时小球做平抛运动，为使小球在运动中不碰到桌子和前壁，则小球刚好运动到桌子右端或车厢右下角．
若小球刚好运动到桌子右端，则
运动的时间为；t=
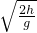=水平位移为：x=v0t=3m
所以车厢运动的位移为s=x-L=2.7m
对车厢有：s=
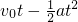
解得：a=15m/s2
F2+kMg=Ma
解得F2=130N
若小球刚好运动到车厢右下角，则
运动的时间为；t=
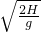=水平位移为：x=v0t=6m
所以车厢运动的位移为s=x-d=4.4m
对车厢有：s=
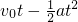
解得：a=20m/s2
F2+kMg=Ma
解得F2=180N
综上可知：为使小球在运动中不碰到桌子和前壁，所加拉力F2应满足130N＜F2＜180N．
答：（1）、求水平推力F1的大小为（M+m）g（k+tanα）；
（2）、为使小球在运动中不碰到桌子和前壁，所加拉力F2应满足130N＜F2＜180N．
分析：（1）对小球进行受力分析，根据牛顿第二定律求得加速度，对整体根据牛顿第二定律即可求解F1的大小；
（2）撤去推力F1同时对车施加水平向左的拉力F2（如虚线所示），小球立即离开斜面向右飞去．此时小球做平抛运动，为使小球在运动中不碰到桌子和前壁，则小球刚好运动到桌子右端或车厢右下角．车厢在F2的作用下做匀减速运动，根据位移关系求出加速度，再根据牛顿第二定律即可求解．
点评：本题主要运用了隔离法和整体法，要根据题目需要选择研究对象运用牛顿第二定律求解，要注意小球离开斜面后做平抛运动，难度较大．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
如图所示，有些地区的铁路由于弯多、弯急，路况复杂，依靠现有车型提速的难度较大，铁路部门通过引进摆式列车来解决转弯半径过小造成的离心问题，摆式列车是集电脑、自动控制等高新技术于一体的新型高速列车．当列车转弯时，在电脑控制下，车厢会自动倾斜，使得车厢受到的弹力FN与车厢底板垂直，FN与车厢重力的合力恰好等于向心力，车厢没有离心侧翻的趋势（车轮内缘还要受到外轨侧向的弹力），当列车行走在直线上时，车厢又恢复原状，就像玩具“不倒翁”一样．它的优点是能够在现有线路上运行，无需对线路等设施进行较大的改造．运行实践表明：摆式列车通过弯道的速度可提高20%---40%，最高可达50%，摆式列车不愧为“曲线冲刺能手”．假设有一超高速摆式列车在水平面内行驶，以360Km/h的速度转弯，转弯半径为2Km，则质量为50Kg 的乘客在拐弯过程中所受到的火车给他的作用力约为（ ）
如图所示，有些地区的铁路由于弯多、弯急、路况复杂，依靠现有车型提速的难度较大，铁路部门通过引进摆式列车来解决转弯半径过小造成的离心问题，摆式列车是集电脑、自动控制等高新技术于一体的新型高速列车．当列车转弯时，在电脑控制下，车厢会自动倾斜，当列车行走在直线上时，车厢又恢复原状，就像玩具“不倒翁”一样．它的优点是能够在现有线路上运行，无需对线路等设施进行较大的改造．运行实践表明：摆式列车通过弯道的速度可提高20%-40%，最高可达50%，摆式列车不愧为“曲线冲刺能手”．假设有一超高速摆式列车在水平面内行驶，以360km/h的速度转弯，转弯半径为2Km，则质量为50kg的乘客在拐弯过程中所受到的火车给他的作用力约为（ ）
=0 .20。在车厢A的正前方轨道上放着车厢B，且A的总质量（不包括小物块）与车厢B的质量相等，两车厢碰撞挂接后连在一起，假设此后它们始终以共同的速度匀速前进（取g=10m/s2）