题目内容
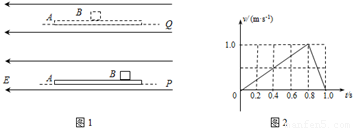
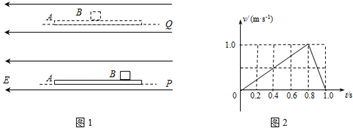
如图1所示，一个质量为0.1kg、电荷量为+1.0×10-6C的小滑块B，放在足够长的粗糙绝缘板A上．用手托住A置于水平向左的匀强电场中，保持A板水平，A、B均静止．现将板A从图中位置P竖直向上托至Q处，其运动的速度随时间变化的图线如图2所示，由于板A的运动，滑块B相对于板A滑动，在板A从位置P运动到Q处的时间内，B相对于A运动了0.02m，板A静止后，滑块B继续在板A上运动了0.02m．取g=10m/s2，求：（1）绝缘板A从P到Q的两个运动过程中的加速度大小分别为多少？
（2）滑块B与板A间的动摩擦因数以及电场强度的大小．
【答案】分析：（1）根据v-t的图象，结合加速度的定义式：
即可计算出两个加速度；
（2）物块B运动的时间、位移已知，属于已知物体的运动求物体的受力，应用牛顿第二定律和运动学的方程，求得物块B运动的加速度，再对B进行受力分析，结合受力分析求得滑块B与板A间的动摩擦因数以及电场强度的大小．
解答：解：（1）设绝缘板A匀加速和匀减速运动过程中的加速度大小分别为a1和a2，由绝缘板A运动的速度随时间变化的图象2可知，加速运动的时间t1=0.8s，减速运动的时间为t2=0.2s，
所以：加速过程中：
减速过程中：
（2）以滑块B为研究对象：
分析：当板A做匀加速运动时，滑块B处于超重状态，滑块B不会相对于A板滑动，当板A做匀减速运动时，滑块B处于失重状态而滑动，设滑块B在水平方向的加速度为a3，
由题意得：
代入数据解得：
受力分析如图1所示：
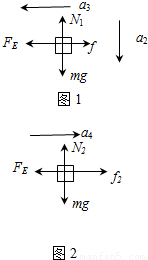
水平方向：FE-f1=ma3
竖直方向：mg-N1=ma2
又f1=μN1
代人数据得：N1=0.5N
所以，A板静止时，滑块B的速度：vB=a3t2=1.0×0.2m/s=0.2m/s
板A静止后，滑块B做匀减速直线运动，设滑块B在水平方向的加速度为a4，
由题意得：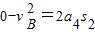
代入数据解得：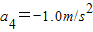
受力分析如图2所示：
水平方向：FE-f2=ma4
竖直方向：mg-N2=0
又：f2=μN2
代入数据解得：N2=1.0N
联立方程（1）、（2）得：μ=0.4；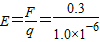
N/C=3×105N/C
答：（1）绝缘板A从P到Q的两个运动过程中的加速度大小分别为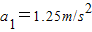
；
；
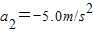（2）滑块B与板A间的动摩擦因数μ=0.4，电场强度的大小3×105N/C．
点评：该题属于已知物体的运动求物体的受力的类型，正确分析物体的加速度是解题的关键．
即可计算出两个加速度；（2）物块B运动的时间、位移已知，属于已知物体的运动求物体的受力，应用牛顿第二定律和运动学的方程，求得物块B运动的加速度，再对B进行受力分析，结合受力分析求得滑块B与板A间的动摩擦因数以及电场强度的大小．
解答：解：（1）设绝缘板A匀加速和匀减速运动过程中的加速度大小分别为a1和a2，由绝缘板A运动的速度随时间变化的图象2可知，加速运动的时间t1=0.8s，减速运动的时间为t2=0.2s，
所以：加速过程中：
减速过程中：
（2）以滑块B为研究对象：
分析：当板A做匀加速运动时，滑块B处于超重状态，滑块B不会相对于A板滑动，当板A做匀减速运动时，滑块B处于失重状态而滑动，设滑块B在水平方向的加速度为a3，
由题意得：
代入数据解得：
受力分析如图1所示：
水平方向：FE-f1=ma3
竖直方向：mg-N1=ma2
又f1=μN1
代人数据得：N1=0.5N
所以，A板静止时，滑块B的速度：vB=a3t2=1.0×0.2m/s=0.2m/s
板A静止后，滑块B做匀减速直线运动，设滑块B在水平方向的加速度为a4，
由题意得：
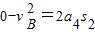
代入数据解得：
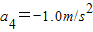
受力分析如图2所示：
水平方向：FE-f2=ma4
竖直方向：mg-N2=0
又：f2=μN2
代入数据解得：N2=1.0N
联立方程（1）、（2）得：μ=0.4；
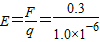N/C=3×105N/C答：（1）绝缘板A从P到Q的两个运动过程中的加速度大小分别为
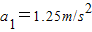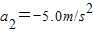；；（2）滑块B与板A间的动摩擦因数μ=0.4，电场强度的大小3×105N/C．
点评：该题属于已知物体的运动求物体的受力的类型，正确分析物体的加速度是解题的关键．
练习册系列答案
口算能手系列答案
相关题目
（2011?崇明县二模）如图1所示，一个质量m=0.1kg的正方形金属框总电阻R=0.5Ω，金属框放在表面绝缘且光滑的斜面顶端（金属框上边与AA′重合），自静止开始沿斜面下滑，下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端（金属框下边与BB’重合），设金属框在下滑过程中的速度为v，与此对应的位移为s，那么v2-s图象（记录了线框运动全部过程）如图2所示，已知匀强磁场方向垂直斜面向上．试问：（g取10m/s2）
的物块，沿固定斜面匀速下滑，斜面的倾角为
，物体与斜面间的动摩擦因数为
，则物块对斜面的作用力为（ ）
，沿斜面向下. B、
，竖直向下.
，沿斜面向上. D、