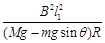题目内容
如图所示,平行金属极板A、B水平放置,A板带正电,B板带负电,两板间的电压为U,距离为2d,一个半径为d的绝缘光滑半圆形轨道,竖直放置在两极板中,轨道最高点、圆心O的连线与极板平行.在轨道最高点边缘处有一质量为m,电量为+ q的小球,由静止开始下滑。重力加速度为g。求:
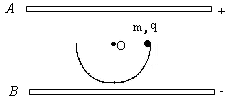
(1)小球到达最低点时的速度大小;
(2)小球经过最低点时对轨道压力的大小。

(1)小球到达最低点时的速度大小;
(2)小球经过最低点时对轨道压力的大小。
(1)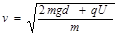 (2)
(2)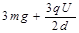
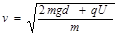 (2)
(2)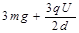
试题分析:(1)由动能定理
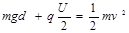 (2分)
(2分)从而求得加速后的速度为
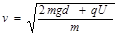 (2分)
(2分)(2)如图,
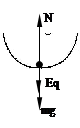
重力、电场力及轨道给小球的支持力的合力提供向心力
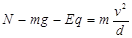 (2分)
(2分)得N=
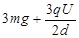 (1分)
(1分)由牛顿第三定律得 对轨道的压力为
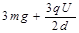 (1分)
(1分)点评:本题难度中等,综合性比较强,首先判断受力情况,在分析做功情况,要想求得圆周运动中最低点对轨道压力大小,就要知道最低点小球速度大小,从而判断出采用动能定理和圆周运动的向心力公式

练习册系列答案
相关题目
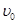 射入电场,经过x轴上的N(2b,0)点。求:
射入电场,经过x轴上的N(2b,0)点。求:


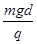

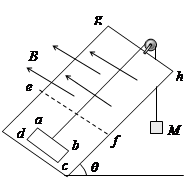
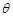 ,斜面上放置一矩形导体线框
,斜面上放置一矩形导体线框 ,
,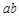 边的边长为
边的边长为 ,
,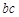 边的边长为
边的边长为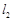 ,线框的质量为
,线框的质量为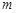 ,电阻为
,电阻为 ,线框通过绝缘细线绕过光滑的滑轮与重物相连,重物质量为
,线框通过绝缘细线绕过光滑的滑轮与重物相连,重物质量为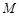 ,斜面上
,斜面上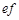 线(
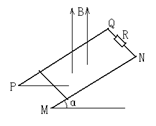
线( ,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的
,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的