题目内容
15.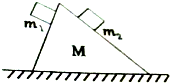 质量分别为m1和m2的两木块静止放在质量为M的斜面上,如图所示,M对地面的压力大小是(m1+m2+M)g,若m1和m2分别沿斜面匀速下滑,在下滑过程中M对地面的压力大小是(m1+m2+M)g.
质量分别为m1和m2的两木块静止放在质量为M的斜面上,如图所示,M对地面的压力大小是(m1+m2+M)g,若m1和m2分别沿斜面匀速下滑,在下滑过程中M对地面的压力大小是(m1+m2+M)g.
分析 对木块和斜面整体为研究对象受力分析,根据平衡条件结合牛顿第三定律求解即可.
解答 解:两木块和斜面都处于静止状态,把两个木块和斜面看成一个整体,受重力、支持力,
竖直方向受力平衡:N=(m1+m2+M)g
若m1和m2分别沿斜面匀速下滑,加速度为零,则可以把两个木块和斜面看成一个整体,受重力、支持力,
竖直方向受力平衡:N′=(m1+m2+M)g
根据牛顿第三定律可知,两种情况下,M对地面的压力大小都是(m1+m2+M)g.
故答案为:(m1+m2+M)g;(m1+m2+M)g
点评 只要物体相互作用且加速度相同,即可作为整体法处理,此题较为典型,应熟记.

练习册系列答案
相关题目
5.一做匀变速直线运动的物体,前两秒通过的位移为2.0米,第五秒通过的位移为3.1米,则该物体的初速度加速度各为( )
| A. | 0.4m/s 0.6m/s2 | B. | 0.6m/s 0.4m/s2 | C. | 0.1m/s 0.9m/s2 | D. | 0.9m/s 0.1m/s2 |
6.在同一地点,质量不同的两个物体从同一高度同时开始做自由落体运动,则( )
| A. | 质量大的物体先落地 | B. | 质量小的物体先落地 | ||
| C. | 两个物体同时落地 | D. | 质量大的物体下落的加速度小 |
20.一蹦极运动员身系弹性蹦极绳从水面上方的高台上静止下落,到最低点时距水面还有数米距离.假定空气阻力可忽略,运动员可视为质点,下列说法正确的是( )
| A. | 蹦极过程中,运动员和地球组成的系统机械能守恒 | |
| B. | 蹦极绳张紧后的下落过程中,运动员的重力势能和弹性绳的弹性势能的和先减小再增大 | |
| C. | 蹦极绳张紧后的下落过程中,重力做功等于重力势能的减少量,且重力势能的改变量与重力势能零点的选取有关 | |
| D. | 运动员到达最低点前,先加速后减速,在最低时速度为零,加速度为最大,且a>g |
 如图所示,质量为m=4kg的物体与水平地面间的动摩擦因数μ=0.3,现用与水平方向成θ=37°的力F拉物体,使物体在水平地面上匀速运动,求:
如图所示,质量为m=4kg的物体与水平地面间的动摩擦因数μ=0.3,现用与水平方向成θ=37°的力F拉物体,使物体在水平地面上匀速运动,求: 在“研究两个共点力合成“的实验中得到如图所示的合力F与两个分力的夹角的关系图.问:
在“研究两个共点力合成“的实验中得到如图所示的合力F与两个分力的夹角的关系图.问: