题目内容
在真空中的光滑水平绝缘面上有一带电小滑块.开始时滑块静止.若在滑块所在空间加一水平匀强电场E1,持续一段时间后立即换成与E1相反方向的匀强电场E2.当电场E2与电场E1持续时间相同时,滑块恰好回到初始位置,且具有动能Ek.在上述过程中,E1对滑块的电场力做功为W1,产生的加速度大小为a1;E2对滑块的电场力做功为W2,产生的加速度大小为a2.则( )
分析:根据题意求出两过程末速度大小,然后应用加速度定义式、动能定理分析答题.
解答:解:由题意知,两个过程经过相同的时间t,发生的位移大小相等,方向相反.设第一过程末速度为v,第二过程末速度大小为v′,
根据上面的分析知两过程的平均速度大小相等,
=
,v′=2v;
A、加速度a1=
,a2=
=
=
,则a2=3a1,故AB错误;
C、根据动能定理有:W1=
mv2,W2=
mv′2-
mv2=3
mv2=3W1,
滑块回到初位置的动能Ek=
mv′2=4
mv2,则W1=0.25Ek,W1=0.75Ek,故C正确,D错误;
故选:C.
根据上面的分析知两过程的平均速度大小相等,
| v |
| 2 |
| v′-v |
| 2 |
A、加速度a1=
| v |
| t |
| v′-v |
| t |
| 2v-(-v) |
| t |
| 3v |
| t |
C、根据动能定理有:W1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
滑块回到初位置的动能Ek=
| 1 |
| 2 |
| 1 |
| 2 |
故选:C.
点评:应用匀变速运动的平均速度公式、动能定理即可正确解题,要注意充分挖掘题目所给信息.

练习册系列答案
相关题目
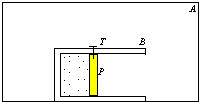
 (2011?沧州二模)如图所示,在真空容器A的水平底部固定着一个绝热气缸B,绝热活塞P将一部分理想气体封闭在气缸内,气缸内壁光滑,当提起梢子T,活塞在气缸内向右运动的过程中,( )
(2011?沧州二模)如图所示,在真空容器A的水平底部固定着一个绝热气缸B,绝热活塞P将一部分理想气体封闭在气缸内,气缸内壁光滑,当提起梢子T,活塞在气缸内向右运动的过程中,( )