题目内容
 如图所示为一根弹簧弹力F与形变量x的关系图线:
如图所示为一根弹簧弹力F与形变量x的关系图线:(1)该弹簧的劲度系数为
(2)将此弹簧从原长拉伸6cm时,它的弹性势能为
(3)将此弹簧从原长压缩4cm时,它的弹性势能为
分析:由胡克定律:F=kx,可知F-x图象的斜率表示弹簧劲度系数,弹性势能的表达式为:EP=
,由此可计算弹簧形变之后的弹性势能.
| kx2 |
| 2 |
解答:解:(1)由胡克定律:F=kx,可知F-x图象的斜率表示弹簧劲度系数,故该弹簧的劲度系数为:k=
N/m=500N/m.
(2)弹性势能的表达式为:EP=
,故将此弹簧从原长拉伸6cm时,它的弹性势能为:EP=
J=0.9J.
(3)弹性势能的表达式为:EP=
,故将此弹簧从原长压缩4cm时,它的弹性势能为:EP=
J=0.4J.
故答案为:(1)500; (2)0.9; (3)0.4.
| 10 |
| 2×10-2 |
(2)弹性势能的表达式为:EP=
| kx2 |
| 2 |
| 500×0.062 |
| 2 |
(3)弹性势能的表达式为:EP=
| kx2 |
| 2 |
| 500×0.042 |
| 2 |
故答案为:(1)500; (2)0.9; (3)0.4.
点评:本题重点是要知道弹性势能的表达式,这个好像在高中不要求会计算弹性势能(可能不同省份不一样,我知道我们省教材没有弹性势能的要求,也不给公式.),其次要知道x指形变量,包含压缩量和伸长量.

练习册系列答案
相关题目
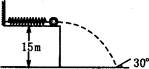
 如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则弹簧被压缩时具有的弹性势能为(g=10m/s2)( )
如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则弹簧被压缩时具有的弹性势能为(g=10m/s2)( ) 如图所示,在高h为5m的光滑平台上有一个质量为0.2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧,当烧断细线时.小球被弹出,小球落地时的速度方向与水平方向成45°.求
如图所示,在高h为5m的光滑平台上有一个质量为0.2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧,当烧断细线时.小球被弹出,小球落地时的速度方向与水平方向成45°.求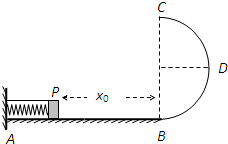 如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BDC在B处平滑连接,B、C分别为半圆轨道的最低点和最高点,D为半圆轨道的最右端.一个质量m的小物体P被一根细线拴住放在水平轨道上,细线的左端固定在竖直墙壁上.在墙壁和P之间夹一根被压缩的轻弹簧,此时P到B点的距离为x0.物体P与水平轨道间的动摩擦因数为μ,半圆轨道半径为R.现将细线剪断,P被弹簧向右弹出后滑上半圆轨道,恰好能通过C点.试求:
如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BDC在B处平滑连接,B、C分别为半圆轨道的最低点和最高点,D为半圆轨道的最右端.一个质量m的小物体P被一根细线拴住放在水平轨道上,细线的左端固定在竖直墙壁上.在墙壁和P之间夹一根被压缩的轻弹簧,此时P到B点的距离为x0.物体P与水平轨道间的动摩擦因数为μ,半圆轨道半径为R.现将细线剪断,P被弹簧向右弹出后滑上半圆轨道,恰好能通过C点.试求: