题目内容
10.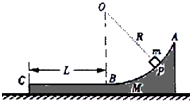 如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑$\frac{1}{4}$圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点.一可视为质点的物块,其质量m=0.2kg,与BC间的动摩擦因数μ=0.4.工件质量M=0.8kg,与地面间的摩擦不计.(取g=10m/s2)
如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑$\frac{1}{4}$圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点.一可视为质点的物块,其质量m=0.2kg,与BC间的动摩擦因数μ=0.4.工件质量M=0.8kg,与地面间的摩擦不计.(取g=10m/s2)(1)若工件固定,将物块由P点无初速度释放,滑至C点时恰好静止,求P、C两点间的高度差h.
(2)若将一水平恒力F作用于工件,使物块仍在P点与工件保持相对静止,一起向左做匀加速直线运动.
①求F的大小.
②当速度v=5m/s时,使工件立刻停止运动(即不考虑减速的时间和位移),物块飞离圆弧轨道落至BC段,求物块的落点与B点间的距离.
分析 (1)物块从P点下滑经B点至C点的整个过程,根据动能定理求解
(2)对物体、工件和物体整体分析,根据牛顿第二定律求解
(3)根据平抛运动的规律和几何关系求解.
解答 解(1)物块从P点下滑经B点至C点的整个过程,根据动能定理得:
mgh-μmgL=0
代入数据得:
h=0.2m…①
(2)①设物块的加速度大小为a,P点与圆心的连线与竖直方向间的夹角为θ,由几何关系可得
cosθ=$\frac{R-h}{R}$…②
根据牛顿第二定律,对物体有
mgtanθ=ma…③
对工件和物体整体有
F=(M+m)a…④
联立①②③④式,代入数据得
F=9.5N…⑤
②设物体平抛运动的时间为t,水平位移为x1,物块落点与B间的距离为 x2,由运动学公式可得
h=$\frac{1}{2}{gt}^{2}$…⑥
x1=vt…⑦
x2=x1-Rsinθ…⑧
联立①②⑥⑦⑧式,代入数据得
x2=0.4m
答:(1)P、C两点间的高度差是0.2m;
(2)F的大小是9.5N;
(3)物块的落点与B点间的距离是0.4m.
点评 该题考查了动能定理、牛顿第二定律、平抛运动的规律多个知识点,关键要对物体进行受力和过程分析.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
18. 两个质点甲与乙,同时由同一地点向同一方向做直线运动,它们的速度一时间图象如图所示.则下列说法中正确的是:( )
两个质点甲与乙,同时由同一地点向同一方向做直线运动,它们的速度一时间图象如图所示.则下列说法中正确的是:( )
 两个质点甲与乙,同时由同一地点向同一方向做直线运动,它们的速度一时间图象如图所示.则下列说法中正确的是:( )
两个质点甲与乙,同时由同一地点向同一方向做直线运动,它们的速度一时间图象如图所示.则下列说法中正确的是:( )| A. | 在第2s 末甲、乙相遇; | B. | 在第2s 末甲、乙速度相等 | ||
| C. | 在2s 内,甲的平均速度比乙的小 | D. | 在3s内,甲的平均速度比乙的小 |
5.下列说法中正确的是( )
| A. | 牛顿最早通过理想斜面实验得出力不是维持物体运动的原因 | |
| B. | 牛顿发现了万有引力定律,并测出了引力常量 | |
| C. | 维持物体运动状态不变的性质是惯性 | |
| D. | 法拉第发现了通电导线周围存在磁场的现象 |
15.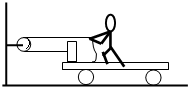 如图中,人和车的质量分别为m1、m2,人用水平力F拉绳子,图中两段绳子都处于水平方向,不计滑轮质量及摩擦,若人和车相对静止,则车的加速度大小为( )
如图中,人和车的质量分别为m1、m2,人用水平力F拉绳子,图中两段绳子都处于水平方向,不计滑轮质量及摩擦,若人和车相对静止,则车的加速度大小为( )
 如图中,人和车的质量分别为m1、m2,人用水平力F拉绳子,图中两段绳子都处于水平方向,不计滑轮质量及摩擦,若人和车相对静止,则车的加速度大小为( )
如图中,人和车的质量分别为m1、m2,人用水平力F拉绳子,图中两段绳子都处于水平方向,不计滑轮质量及摩擦,若人和车相对静止,则车的加速度大小为( )| A. | 0 | B. | $\frac{F}{{m}_{2}}$ | C. | $\frac{F}{{m}_{1}+{m}_{2}}$ | D. | $\frac{2F}{{m}_{1}+{m}_{2}}$ |
2.以下计时数据指时间的是( )
| A. | 开往天津的飞机于13时35分正点出发 | |
| B. | 某运动员的十米成绩是1s | |
| C. | 1997年7月1日零时,中国对香港恢复行使主权 | |
| D. | 某场足球赛早上9:30分正式开始 |
20.某兴趣小组欲通过测定工业污水(含多种重金属离子)的电阻率来判断某工厂废水是否达到排放标准(一般工业废水电阻率的达标值ρ≥200Ω•m).如图1所示为该同学所用盛水容器,其左、右两侧面为金属薄板(电阻极小),其余四面由绝缘材料制成,左右两侧带有接线柱.容器内表面长a=40cm,宽b=20cm,高c=10cm.将水样注满容器后,进行以下操作:
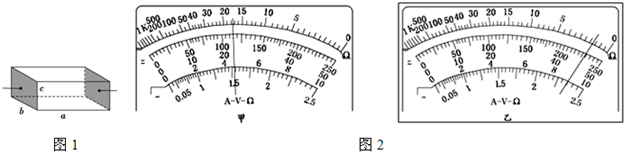
(1)分别用多用电表欧姆挡的“×100”、“×1k”两挡粗测水样的电阻值时,表盘上指针分别如图2甲、乙所示,则所测水样的电阻约为1750Ω.
(2)为更精确地测量所取水样的电阻,该小组从实验室中找到如下实验器材:
A.电流表(量程5mA,电阻RA为50Ω)
B.电压表(量程15V,电阻RV约为10kΩ)
C.滑动变阻器(0~20Ω,额定电流1A)
D.电源(12V,内阻约10Ω)
E.开关一只、导线若干
请在实物图3中完成电路连接.

(3)正确连接电路后,闭合开关,测得一组U、I数据;再调节滑动变阻器,重复上述测量步骤,测出一系列数据如表所示,请在如图4实所示的坐标纸中作出UI关系图线.
(4)由以上测量数据可以求出待测水样的电阻率为109.8Ω•m.据此可知,所得水样在电阻率这一指标上不达标(选填“达标”或“不达标”).

(1)分别用多用电表欧姆挡的“×100”、“×1k”两挡粗测水样的电阻值时,表盘上指针分别如图2甲、乙所示,则所测水样的电阻约为1750Ω.
(2)为更精确地测量所取水样的电阻,该小组从实验室中找到如下实验器材:
A.电流表(量程5mA,电阻RA为50Ω)
B.电压表(量程15V,电阻RV约为10kΩ)
C.滑动变阻器(0~20Ω,额定电流1A)
D.电源(12V,内阻约10Ω)
E.开关一只、导线若干
请在实物图3中完成电路连接.

(3)正确连接电路后,闭合开关,测得一组U、I数据;再调节滑动变阻器,重复上述测量步骤,测出一系列数据如表所示,请在如图4实所示的坐标纸中作出UI关系图线.
| U/V | 2.0 | 3.8 | 6.8 | 8.0 | 10.2 | 11.6 |
| I/mA | 0.73 | 1.36 | 2.20 | 2.89 | 3.66 | 4.15 |
 在光滑绝缘的水平面上放置一个质量m=0.2kg、带电荷量q=5×10-4 C的小球,小球系在长L=0.5m的绝缘细线上,线的另一端固定在O点.整个装置置于匀强电场中,电场方向与水平面平行且沿OA方向,如图所示(此图为俯视图).现给小球一个初速度使其绕O点做圆周运动,小球经过A点时细线的张力F=140N,小球在运动过程中,最大动能比最小动能大20J,小球可视为质点.
在光滑绝缘的水平面上放置一个质量m=0.2kg、带电荷量q=5×10-4 C的小球,小球系在长L=0.5m的绝缘细线上,线的另一端固定在O点.整个装置置于匀强电场中,电场方向与水平面平行且沿OA方向,如图所示(此图为俯视图).现给小球一个初速度使其绕O点做圆周运动,小球经过A点时细线的张力F=140N,小球在运动过程中,最大动能比最小动能大20J,小球可视为质点. 如图,一光滑的半径为R=0.4m的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则:
如图,一光滑的半径为R=0.4m的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则: