题目内容
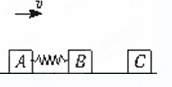
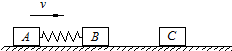 两物块A、B用轻弹簧相连,质量均为2kg,初始时弹簧处于原长,A、B两物块都以v=6m/s的速度在光滑的水平地面上运动,质量4kg的物块C静止在前方,如图所示.B与C碰撞后二者立刻会粘在一起运动.求在以后的运动中:
两物块A、B用轻弹簧相连,质量均为2kg,初始时弹簧处于原长,A、B两物块都以v=6m/s的速度在光滑的水平地面上运动,质量4kg的物块C静止在前方,如图所示.B与C碰撞后二者立刻会粘在一起运动.求在以后的运动中:(1)B与C碰撞后二者刚粘在一起运动时BC的速度
(2)系统中弹性势能的最大值是多少?
(3)A物块的速度有可能向左吗?试用能量的观点证明之.?
分析:(1)B与C发生碰撞后,根据动量守恒求出物BC的速度.
(2)分过程研究:BC碰撞过程,由动量守恒求出碰后两者的共同速度.当A、B、C三者的速度相等时弹簧的弹性势能最大,由系统的机械能守恒求出最大的弹性势能.
(3)设A的速度能向左,根据系统的动量守恒,得到B的速度范围,分析三个物体的总动能与系统总机械能的关系,判断A的速度向左是否可能.
(2)分过程研究:BC碰撞过程,由动量守恒求出碰后两者的共同速度.当A、B、C三者的速度相等时弹簧的弹性势能最大,由系统的机械能守恒求出最大的弹性势能.
(3)设A的速度能向左,根据系统的动量守恒,得到B的速度范围,分析三个物体的总动能与系统总机械能的关系,判断A的速度向左是否可能.
解答:解:(1)B、C碰撞时B、C组成的系统动量守恒,设碰后瞬间B、C两者速度为vBC,则?mBv=(mB+mC)vBC
vBC=
=2m/s?
(2)ABC速度相同时弹簧的弹性势能最大,设为Ep,?
A、B、C三者组成的系统动量守恒,(mA+mB)v=(mA+mB+mC)vABC
解得vABC=
m/s=3m/s
根据能量守恒Ep=
(mB+mC)
+
mAv2-
(mA+mB+mC)vABC2
=
×(2+4)×22+
×2×62-
×(2+2+4)×32=12J
(3)A不可能向左运动
取向右为正,由系统动量守恒,(mA+mB)v=mAvA′+(mB+mC)vBC′
若A向左,vA′<0,即得vBC′>4m/s
则A、B、C动能之和?E′=
mAv
+
(mB+mC)v
>48J
而系统的总机械能?E=Ep+
(mA+mB+mC)vABC2=12+36=48J
根据能量守恒定律,E'>E是不可能的
答:(1)B与C碰撞后二者刚粘在一起运动时BC的速度大小是2m/s;
(2)A、B、C及弹簧组成的系统中弹性势能的最大值是12J
(3)A的速度不可能向左.
vBC=
| 2×6 |
| 2+4 |
(2)ABC速度相同时弹簧的弹性势能最大,设为Ep,?
A、B、C三者组成的系统动量守恒,(mA+mB)v=(mA+mB+mC)vABC
解得vABC=
| (2+2)×6 |
| 2+2+4 |
根据能量守恒Ep=
| 1 |
| 2 |
| v | 2 BC |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)A不可能向左运动
取向右为正,由系统动量守恒,(mA+mB)v=mAvA′+(mB+mC)vBC′
若A向左,vA′<0,即得vBC′>4m/s
则A、B、C动能之和?E′=
| 1 |
| 2 |
| ′ | 2 A |
| 1 |
| 2 |
| ′ | 2 BC |
而系统的总机械能?E=Ep+
| 1 |
| 2 |
根据能量守恒定律,E'>E是不可能的
答:(1)B与C碰撞后二者刚粘在一起运动时BC的速度大小是2m/s;
(2)A、B、C及弹簧组成的系统中弹性势能的最大值是12J
(3)A的速度不可能向左.
点评:对于是含有弹簧的系统,抓住系统的合外力为零,遵守两大守恒:动量守恒和机械能守恒进行研究.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
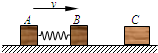 两物块A、B用轻弹簧相连,质量均为2kg,初始时弹簧处于原长,A、B两物块都以v=6m/s的速度在光滑的水平地面上运动,质量4kg的物块C静止在前方,如图所示.B与C碰撞后二者会粘在一起运动.求在以后的运动中:
两物块A、B用轻弹簧相连,质量均为2kg,初始时弹簧处于原长,A、B两物块都以v=6m/s的速度在光滑的水平地面上运动,质量4kg的物块C静止在前方,如图所示.B与C碰撞后二者会粘在一起运动.求在以后的运动中: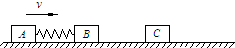 两物块A、B用轻弹簧相连,质量均为2kg,初始时弹簧处于原长,A、B两物块都以v=6m/s的速度在光滑的水平地面上运动,质量4kg的物块C静止在前方,如图所示.B与C碰撞后二者立刻会粘在一起运动.求在以后的运动中:
两物块A、B用轻弹簧相连,质量均为2kg,初始时弹簧处于原长,A、B两物块都以v=6m/s的速度在光滑的水平地面上运动,质量4kg的物块C静止在前方,如图所示.B与C碰撞后二者立刻会粘在一起运动.求在以后的运动中: