题目内容
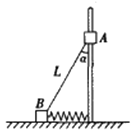
【题目】如图所示,水平直轨道AC的长度为L=8m,AC中点B正上方有一探测器,C处有一竖直挡板D.现使物块Pl沿轨道向右以速度Vl与静止在A处的物块P2正碰,碰撞后,P1与P2粘成组合体P.以Pl、P2碰撞时刻为计时零点,探测器只在t1=2s至t2=4s内工作。已知物块Pl、P2的质量均力m=1kg,Pl、P2和P均视为质点,不计空气阻力,重力加速度g取10m/s2。
(1)若v1=8m/s,P恰好不与挡板发生碰撞,求P与轨道AC间的动摩擦因数;
(2)若P与挡板发生弹性碰撞后,并能在探测器工作时间内通过B点,求V1的取值范围;
(3)在满足(2)的条件下,求P向左经过A点时的最大动能。

【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)设Pl、P2碰撞后,P的速度为v,根据动量守恒:mv1=2mv
解得:v=4 m/s
P恰好不与挡板发生碰撞,即P到达C点速度恰好减为零
根据动能定理:![]()
代入解得:![]()
(2)由于P与档板的碰撞为弹性碰撞,P在AC间等效为匀减速运动,设P的加速度大小为a。
根据牛顿第二定律:μ2mg=2ma
P返回经B点,根据匀变速直线运动的规律:![]()
由题意知,物块P在2~4s内经过B点,代入数据解得![]()
再结合mv1=2mv
得![]()
(3)设P向左经过A点时的速度为v2,由速度位移公式:![]()
联立解得P向左经过A点的最大动能为:![]() J
J

练习册系列答案
相关题目