题目内容
 甲和乙两个质点同时同地向同一方向作直线运动,它们的v-t图象如图,则下面说法正确的是( )
甲和乙两个质点同时同地向同一方向作直线运动,它们的v-t图象如图,则下面说法正确的是( )分析:速度的大小表示物体运动的快慢.根据图线“面积”分析什么时刻乙追上甲.根据两物体速度的大小,分析什么两者距离的变化,确定何时两者相距最远.由“面积”求出乙追上甲时离出发点的距离.
解答:解:
A、在前2s内甲的速度大于乙的速度,甲比乙运动快;在后2s内乙的速度大于甲的速度,乙比甲运动快.故A错误.
B、在2s时刻甲乙的速度相同,甲的位移大于乙的位移,而两个质点是同时同地向同一方向作直线运动的,所以在2s时刻乙还没有追上甲.故B错误.
C、在前2s内甲的速度大于乙的速度,两者距离增大,在后2s内乙的速度大于甲的速度,两者距离减小,则在0到4s的时间内,2s时刻甲和乙相距最远.故C正确.
D、由图看出,4s末时刻两质点的位移相等,乙追上了甲,此时离出发点的距离为S=v甲t=10×4m=40m.故D正确.
故选CD
A、在前2s内甲的速度大于乙的速度,甲比乙运动快;在后2s内乙的速度大于甲的速度,乙比甲运动快.故A错误.
B、在2s时刻甲乙的速度相同,甲的位移大于乙的位移,而两个质点是同时同地向同一方向作直线运动的,所以在2s时刻乙还没有追上甲.故B错误.
C、在前2s内甲的速度大于乙的速度,两者距离增大,在后2s内乙的速度大于甲的速度,两者距离减小,则在0到4s的时间内,2s时刻甲和乙相距最远.故C正确.
D、由图看出,4s末时刻两质点的位移相等,乙追上了甲,此时离出发点的距离为S=v甲t=10×4m=40m.故D正确.
故选CD
点评:本题匀加速直线运动追及匀速直线运动的问题,抓住图线的斜率等于加速度、“面积”等于位移来分析.

练习册系列答案
相关题目

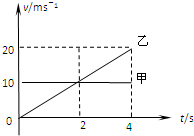 甲和乙两个质点同时同地向同一方向作直线运动,它们的v-t图象如图,则下面说法正确的是
甲和乙两个质点同时同地向同一方向作直线运动,它们的v-t图象如图,则下面说法正确的是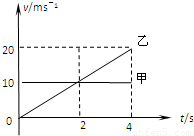 甲和乙两个质点同时同地向同一方向作直线运动,它们的v-t图象如图,则下面说法正确的是( )
甲和乙两个质点同时同地向同一方向作直线运动,它们的v-t图象如图,则下面说法正确的是( )