题目内容
物体A 、B、 C均静止在同一水平面上,它们的质量分别为mA、 mB、 mC,与平面的动摩擦因数分别为μA、μB 、μC,用平行于水平面的拉力F分别拉物体A、B、C所得加速度a与F的关系图线如图,对应的直线甲、乙、丙所示,甲、乙直线平行,则以下说法正确的是( )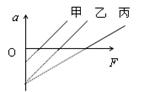
A.μA< μB mA =mB
B.μB >μC mB >mC
C.μB =μC mB >mC
D.μA<μC mA< mC
AD
解析试题分析:根据牛顿第二定律有:F-umg=ma,得 a=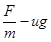 ,由此可知:图象斜率为质量的倒数,在纵轴上的截距大小为:ug, 故由图象可知:μA<μB=μC,mA=mB<mC,所以本题选择AD。
,由此可知:图象斜率为质量的倒数,在纵轴上的截距大小为:ug, 故由图象可知:μA<μB=μC,mA=mB<mC,所以本题选择AD。
考点:牛顿第二定律 匀变速直线运动图象 摩擦力

某物体做匀变速直线运动,其位移与时间的关系为x=0.5t+t2,则当物体速度为3m/s时,物体已运动的时间为
| A.1.25s | B.2.5s | C.3s | D.6s |
一物体由静止沿一足够长光滑斜面匀加速下滑距离为L时,速度为v,此后继续下滑,当它的速度增至2v时,它又沿斜面继续下滑的距离是
| A.L | B.2L | C.3L | D.4L |
如图所示,传送带保持1 m/s的速度顺时针转动。现将一质量m=0.5 kg的物体轻轻地放在传送带的a点上,设物体与传送带间的动摩擦因数μ=0.1,a、b间的距离L=2.5 m,则物体从a点运动到b点所经历的时间为 (g取10 m/s2)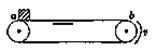
A.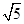 s s | B.(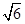 -1) s -1) s |
| C.3 s | D.2.5 s |
物体第1s由静止向东做加速度为1m/s2的匀加速直线运动,第2s加速度方向向西,大小不变,以后每隔1s加速度的方向都改变一次,但大小不变,如此反复只改变加速度的方向,共历时1 min。则在此1min内( )
| A.物体时而向东运动,时而向西运动,在1 min 末静止于初始位置之西 |
| B.物体一直向东运动,从不向西运动,在1 min 末静止于初始位置之东30m的位置 |
| C.物体时而向东运动,时而向西运动,在1 min 末继续向东运动 |
| D.物体一直向东运动,从不向西运动,在1 min 末静止于初始位置之东15m的位置 |
如图所示,一小滑块沿足够长的斜面以初速度v向上做匀减速直线运动,依次经A,B,C,D 到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s .设滑块经C时的速度为vc,则( )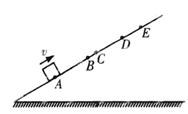
| A.滑块上滑过程中加速度的大小为0.5m/s2 |
| B.vc =6m/s |
| C.DE=3m |
| D.从D到E所用时间为4s |