题目内容
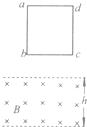
均匀导线制成的电阻为R、质量为m的单匝矩形闭合线框abcd,边长ab=h,ad=L,将线框置于一有界匀强磁场上方某一高度处,如图所示.已知该磁场区域宽度为h,方向沿水平、垂直线框所在平面向里,磁感应强度为B.现使线框由静止自由下落,线框平面保持与磁场方向垂直,且bc边始终保持水平方向.若线框恰好以恒定速度通过磁场,重力加速度为g,空气阻力可忽略不计,求:(1)线框通过磁场过程中产生的焦耳热;
(2)开始下落时线框bc边与磁场上边界的距离;
(3)bc边在磁场区域运动的过程中,a、d两点间的电势差.

【答案】分析:(1)根据能量守恒定律求出线框通过磁场过程中产生的焦耳热.
(2)根据线框在磁场中做匀速直线运动,通过共点力平衡求出线框进入磁场时的速度,再通过速度位移公式求出开始下落时线框bc边与磁场上边界的距离;
(3)根据速度求出切割产生的感应电动势,从而根据欧姆定律求出a、d两点间的电势差.
解答:解:(1)因为线框恰好以恒定速度通过磁场,根据能量守恒定律有:
Q=2mgh.
(2)根据mg=BIL=
解得v= .
.
根据v2=2gh,解得h= .
.
(3)bc边在磁场区域运动的过程中,切割产生的感应电动势E=BLv= .
.
则a、d两点间的电势差 .
.
答:(1)线框通过磁场过程中产生的焦耳热为2mgh.
(2)开始下落时线框bc边与磁场上边界的距离为 .
.
(3)a、d两点间的电势差为 .
.
点评:本题考查了电磁感应与力学和能量的综合,难度中等,电磁感应是高考的重点和热点问题,需加强训练.
(2)根据线框在磁场中做匀速直线运动,通过共点力平衡求出线框进入磁场时的速度,再通过速度位移公式求出开始下落时线框bc边与磁场上边界的距离;
(3)根据速度求出切割产生的感应电动势,从而根据欧姆定律求出a、d两点间的电势差.
解答:解:(1)因为线框恰好以恒定速度通过磁场,根据能量守恒定律有:
Q=2mgh.
(2)根据mg=BIL=

解得v=
 .
.根据v2=2gh,解得h=
 .
.(3)bc边在磁场区域运动的过程中,切割产生的感应电动势E=BLv=
 .
.则a、d两点间的电势差
 .
.答:(1)线框通过磁场过程中产生的焦耳热为2mgh.
(2)开始下落时线框bc边与磁场上边界的距离为
 .
.(3)a、d两点间的电势差为
 .
.点评:本题考查了电磁感应与力学和能量的综合,难度中等,电磁感应是高考的重点和热点问题,需加强训练.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
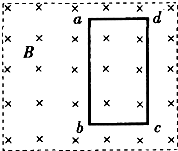 如图所示,在方向垂直于纸面向里,磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd,线框在水平拉力作用下以恒定的速度v沿垂直磁场方向向右运动,运动中线框ab边始终与磁场右边界平行,线框边长ad=l,cd=2l,线框导线的总电阻为R.则线框离开磁场的过程中( )
如图所示,在方向垂直于纸面向里,磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd,线框在水平拉力作用下以恒定的速度v沿垂直磁场方向向右运动,运动中线框ab边始终与磁场右边界平行,线框边长ad=l,cd=2l,线框导线的总电阻为R.则线框离开磁场的过程中( )A、ab间的电压为
| ||
B、ad间的电压为
| ||
C、线框中的电流在ab边产生的热量为
| ||
D、线框中的电流在ad边产生的热量为
|
 (2011?海淀区模拟)均匀导线制成的电阻为R、质量为m的单匝矩形闭合线框abcd,边长ab=h,ad=L,将线框置于一有界匀强磁场上方某一高度处,如图所示.已知该磁场区域宽度为h,方向沿水平、垂直线框所在平面向里,磁感应强度为B.现使线框由静止自由下落,线框平面保持与磁场方向垂直,且bc边始终保持水平方向.若线框恰好以恒定速度通过磁场,重力加速度为g,空气阻力可忽略不计,求:
(2011?海淀区模拟)均匀导线制成的电阻为R、质量为m的单匝矩形闭合线框abcd,边长ab=h,ad=L,将线框置于一有界匀强磁场上方某一高度处,如图所示.已知该磁场区域宽度为h,方向沿水平、垂直线框所在平面向里,磁感应强度为B.现使线框由静止自由下落,线框平面保持与磁场方向垂直,且bc边始终保持水平方向.若线框恰好以恒定速度通过磁场,重力加速度为g,空气阻力可忽略不计,求: