题目内容
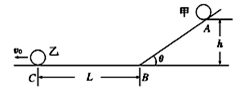
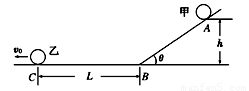
 如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0沿光滑水平面向左匀速运动,C点与斜面底端B处的距离L=0.4m.甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去,甲释放后经过t=1s刚好追上乙,求乙的速度v0.
如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0沿光滑水平面向左匀速运动,C点与斜面底端B处的距离L=0.4m.甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去,甲释放后经过t=1s刚好追上乙,求乙的速度v0.分析:恰好追上表示经过相同的时间,甲乙两球到达同一位置,抓住位移之间的关系根据运动学基本公式即可求解.
解答:解:设小球甲在光滑斜面上运动的加速度为a,运动时间为t1,运动到B处时的速度为v1,从B处到追上小球乙所用时间为t2,则
a=gsin30°=5 m/s2
由
=
得:t1=
=0.2 s
t2=t-t1=0.8 s
v1=at1=1 m/s
v0t+L=v1t2
代入数据解得:v0=0.4 m/s.
答:乙的速度v0为0.4 m/s.
a=gsin30°=5 m/s2
由
| h |
| sin30° |
| 1 |
| 2 |
| at | 2 1 |
|
t2=t-t1=0.8 s
v1=at1=1 m/s
v0t+L=v1t2
代入数据解得:v0=0.4 m/s.
答:乙的速度v0为0.4 m/s.
点评:追击问题要注意抓住时间和位移之间的关系,运用运动学基本公式即可解题.

练习册系列答案
相关题目
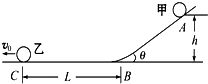 如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0沿光滑水平面向左匀速运动,C点与斜面底端B处的距离L=0.6m.甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去,甲释放后经过t=1s刚好追上乙,求乙的速度v0(g=10m/s2).
如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0沿光滑水平面向左匀速运动,C点与斜面底端B处的距离L=0.6m.甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去,甲释放后经过t=1s刚好追上乙,求乙的速度v0(g=10m/s2).