题目内容
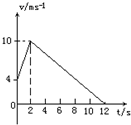 质量为2千克的物体在水平面上做直线运动,在0~2秒内受到跟运动方向相同的拉力作用,之后撤去拉力,运动情况如图所示,根据其运动图线计算拉力做的功等于
质量为2千克的物体在水平面上做直线运动,在0~2秒内受到跟运动方向相同的拉力作用,之后撤去拉力,运动情况如图所示,根据其运动图线计算拉力做的功等于112J
112J
;物体克服阻力做的功等于128J
128J
.分析:速度图象的斜率等于物体的加速度,由数学知识求出斜率,得到加速度.
对匀加速和匀减速两个过程,运用牛顿第二定律求出拉力和滑动摩擦力,根据速度图象的“面积”求出位移,即可求得拉力和摩擦力做功.
对匀加速和匀减速两个过程,运用牛顿第二定律求出拉力和滑动摩擦力,根据速度图象的“面积”求出位移,即可求得拉力和摩擦力做功.
解答:解:
速度图象的斜率等于物体的加速度,则前2秒的加速度a1=
=3m/s2.
2~6秒的加速度大小a2=
=-1m/s2.
对于两段运动过程,由牛顿第二定律得:
F-Ff=ma1 ①
-Ff=ma2 ②
解得:F=8 N,Ff=2N,
前2秒位移:x1=
×(4+10)×2=14m
2秒~12秒位移:x2=
×10×10=50m
拉力做功为 WF=Fx1=112 J,
整个过程中摩擦力做功为WFf=-Ff(x1+x2)=-128 J
物体克服阻力做的功为128J
故答案为:112J,128J;
速度图象的斜率等于物体的加速度,则前2秒的加速度a1=
| 10-4 |
| 2 |
2~6秒的加速度大小a2=
| 0-10 |
| 10 |
对于两段运动过程,由牛顿第二定律得:
F-Ff=ma1 ①
-Ff=ma2 ②
解得:F=8 N,Ff=2N,
前2秒位移:x1=
| 1 |
| 2 |
2秒~12秒位移:x2=
| 1 |
| 2 |
拉力做功为 WF=Fx1=112 J,
整个过程中摩擦力做功为WFf=-Ff(x1+x2)=-128 J
物体克服阻力做的功为128J
故答案为:112J,128J;
点评:本题是速度图象与牛顿第二定律、功等等知识的综合,关键要抓住速度图象的斜率等于物体的加速度.本题也可以根据动能定理求解功.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 质量为2千克的物体在水平面上做直线运动,在0~2秒内受到跟运动方向相同的拉力作用,之后撤去拉力,运动情况如图所示,根据其运动图线计算拉力做的功等于________;物体克服阻力做的功等于________.
质量为2千克的物体在水平面上做直线运动,在0~2秒内受到跟运动方向相同的拉力作用,之后撤去拉力,运动情况如图所示,根据其运动图线计算拉力做的功等于________;物体克服阻力做的功等于________.

