题目内容
 (2013?成都三模)如图所示,水平光滑绝缘桌面距地面高h,x轴将桌面分为I、Ⅱ两个区域,其中,I区域的匀强电场场强为E,方向与ab边及x轴垂直,且平行于桌面;Ⅱ区域是磁感应强度为3
(2013?成都三模)如图所示,水平光滑绝缘桌面距地面高h,x轴将桌面分为I、Ⅱ两个区域,其中,I区域的匀强电场场强为E,方向与ab边及x轴垂直,且平行于桌面;Ⅱ区域是磁感应强度为3
|
(1)小球进入磁场时的速度;
(2)小球飞出ad边的瞬间,速度方向与ad边夹角θ;
(3)小球飞离桌面后,落地点距ad边在地面投影的距离.
分析:(1)小球在电场中运动时,只有电场力做功,大小为qEl,根据动能定理可求得小球进入磁场时的速度;
(2)小球进入磁场后,竖直方向上受到重力和桌面的支持力,两力平衡,小球由洛伦兹力充当向心力在桌面上做匀速圆周运动,画出轨迹(俯视图),根据牛顿第二定律求出半径;速度方向与ad边夹角θ;
(3)小球飞离桌面后做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,由运动学公式求出小球飞行的水平距离.
(2)小球进入磁场后,竖直方向上受到重力和桌面的支持力,两力平衡,小球由洛伦兹力充当向心力在桌面上做匀速圆周运动,画出轨迹(俯视图),根据牛顿第二定律求出半径;速度方向与ad边夹角θ;
(3)小球飞离桌面后做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,由运动学公式求出小球飞行的水平距离.
解答: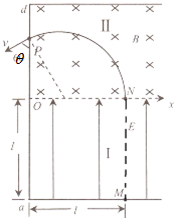 解:(1)小球在电场中沿MN方向做匀加速直线运动,此过程由动能定理,有 qEl=
解:(1)小球在电场中沿MN方向做匀加速直线运动,此过程由动能定理,有 qEl=
mv2 ①
可得小球进入磁场时的速度 v=
,v方向x轴垂直.
(2)小球进入磁场后做匀速圆周运动,轨迹如图所示.
由几何关系可得:R+Rcosθ=l ②
又由洛仑兹力提供向心力,有 qvB=m
③
由②③④式可得:θ=60°
(3)小球飞离桌面后做平抛运动,由平抛规律有 h=
gt2 ④
x=vt ⑤,
d=xsin60°⑥
由①、②、⑤、⑥式可得,小球飞行落地点距ad边的距离为 d=
答:
(1)小球进入磁场时的速度为
;
(2)小球飞出ad边的瞬间,速度方向与ad边夹角θ为60°;
(3)小球飞离桌面后,落地点距ad边在地面投影的距离为
.
 解:(1)小球在电场中沿MN方向做匀加速直线运动,此过程由动能定理,有 qEl=
解:(1)小球在电场中沿MN方向做匀加速直线运动,此过程由动能定理,有 qEl=| 1 |
| 2 |
可得小球进入磁场时的速度 v=
|
(2)小球进入磁场后做匀速圆周运动,轨迹如图所示.
由几何关系可得:R+Rcosθ=l ②
又由洛仑兹力提供向心力,有 qvB=m
| v2 |
| R |
由②③④式可得:θ=60°
(3)小球飞离桌面后做平抛运动,由平抛规律有 h=
| 1 |
| 2 |
x=vt ⑤,
d=xsin60°⑥
由①、②、⑤、⑥式可得,小球飞行落地点距ad边的距离为 d=
|
答:
(1)小球进入磁场时的速度为
|
(2)小球飞出ad边的瞬间,速度方向与ad边夹角θ为60°;
(3)小球飞离桌面后,落地点距ad边在地面投影的距离为
|
点评:本题小球在复合场中运动,分析小球运动受力情况和运动情况是解题的关键,运用动能定理和牛顿第二定律、运动学公式结合即可求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (2013?成都三模)一列简谐横波在x轴上传播,某一时刻的波形如图所示,a、b、c是波上的三个质点,质点a向上运动,该波的频率为2Hz,由此可知( )
(2013?成都三模)一列简谐横波在x轴上传播,某一时刻的波形如图所示,a、b、c是波上的三个质点,质点a向上运动,该波的频率为2Hz,由此可知( ) (2013?成都三模)如图所示,是质量为1kg的物体放在光滑水平面上,受变化的水平方向的外力作用下的v-t图象,由图象可以得出的正确结论是( )
(2013?成都三模)如图所示,是质量为1kg的物体放在光滑水平面上,受变化的水平方向的外力作用下的v-t图象,由图象可以得出的正确结论是( )