题目内容
19.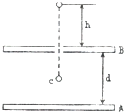 如图所示,带电平行金属板A,B,板间的电势差恒为 U,A板带正电,B板中央有一小孔.一带正电的微粒,带电量为q,质量为m,自孔的正上方 P点(距板高 h)处自由落下,若微粒恰能落至A,B板的正中央C点,则( )
如图所示,带电平行金属板A,B,板间的电势差恒为 U,A板带正电,B板中央有一小孔.一带正电的微粒,带电量为q,质量为m,自孔的正上方 P点(距板高 h)处自由落下,若微粒恰能落至A,B板的正中央C点,则( )| A. | 微粒下落过程中重力做功为g(h+$\frac{d}{2}$)m,电场力做功为qU | |
| B. | 将B板上移少许,微粒仍从 P 点自由落下则一定能到达 C点 | |
| C. | 将A板下移少许,微粒仍从 P 点自由落下则不能经过C点 | |
| D. | 若微粒从距B板高2h处自由下落,则恰好能达到A 板. |
分析 微粒在板间运动电场力做负功,重力做正功,应用动能定理分析答题.
解答 解:A、微粒下落过程重力做功:mg(h+$\frac{d}{2}$),电场力做功为:-q•$\frac{1}{2}$U,故A错误;
B、将B板上移少许,两板间的电场强度E不变,BC间的距离变大,BC间的电势差变大,重力做功不变,将B板上移少许,微粒仍从P点自由落下则不能到达C点,故B错误;
C、将A板下移少许,两板间的电场强度E不变,BC间的距离不变,重力与电场力做功不变,微粒仍从P点自由落下,微粒能经过C点,故C错误;
D、由题微粒恰能落至A,B板的正中央c点过程,由动能定理得:mg(h+$\frac{d}{2}$)-$\frac{1}{2}$qU=0 ①
若微粒从距B板高2h处自由下落,设达到A板的速度为v,则由动能定理得:
mg(2h+d)-qU=$\frac{1}{2}$mv2-0 ②
由①②联立得v=0,即恰好能达到A板,故D正确;
故选:D.
点评 本题根据动能定理研究微粒能否到达A板,也可以根据牛顿第二定律和运动学公式分析.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9. 如图所示,光滑斜面上放一条形磁铁,并在图中所示的位置放一垂直纸面方向的通电导线,要使条形磁铁能静止在光滑斜面上,下列操作正确的是( )
如图所示,光滑斜面上放一条形磁铁,并在图中所示的位置放一垂直纸面方向的通电导线,要使条形磁铁能静止在光滑斜面上,下列操作正确的是( )
 如图所示,光滑斜面上放一条形磁铁,并在图中所示的位置放一垂直纸面方向的通电导线,要使条形磁铁能静止在光滑斜面上,下列操作正确的是( )
如图所示,光滑斜面上放一条形磁铁,并在图中所示的位置放一垂直纸面方向的通电导线,要使条形磁铁能静止在光滑斜面上,下列操作正确的是( )| A. | 若磁铁上端为N极,则导线中电流方向向外 | |
| B. | 若磁铁上端为N极,则导线中电流方向向里 | |
| C. | 若磁铁上端为S极,则导线中电流方向向外 | |
| D. | 若磁铁上端为S极,则导线中电流方向向里 |
10.用波长为λ1和λ2的单色光1和2分别照射金属1和2的表面.色光1照射金属1和2的表面时都有电子射出,色光2照射金属1时有电子射出,照射金属2时没有电子射出.设金属1和2的逸出功为W1和W2,则有( )
| A. | λ1>λ2,W1>W2 | B. | λ1>λ2,W1<W2 | C. | λ1<λ2,W1>W2 | D. | λ1<λ2,W1<W2 |
7.以下列说法中正确的是( )
| A. | 高速运动的物体不容易停下来,所以物体运动速度越大,惯性越大 | |
| B. | 物体只有运动时才体现出惯性 | |
| C. | 乒乓球可以快速抽杀,是因为乒乓球的惯性小的缘故 | |
| D. | 物体的惯性与物体的运动状态无关 |
4.如图,一细光束通过玻璃三棱镜折射后分成a、b、c三束单色光,则这三种单色光中( )


| A. | 光子的能量Ea>Eb>Ec | |
| B. | 在真空中传播的速度的关系是va<vb<vc | |
| C. | 分别通过同一双缝产生的干涉条纹的间距是da>db>dc | |
| D. | 在真空中传播时的波长关系是λa<λb<λc |
8.下列说法正确的是( )
| A. | ${\;}_{7}^{15}$N+${\;}_{1}^{1}$H→${\;}_{6}^{12}$C+${\;}_{2}^{4}$He是α衰变方程 | |
| B. | ${\;}_{1}^{1}$H+${\;}_{1}^{2}$H→${\;}_{2}^{3}$He+γ是核聚变反应方程 | |
| C. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是核裂变反应方程 | |
| D. | ${\;}_{2}^{4}$He+${\;}_{13}^{27}$Al→${\;}_{15}^{30}$P+${\;}_{0}^{1}$n是人工转变方程 |
 十三陵抽水蓄能电站的工作原理是,在用电低谷时,电站利用电网多余电能把水抽到高出蓄水池中,到用电高峰时,再利用蓄水池中的水发电.电站利用十三陵水库为下游水库,在蟒山后上寺沟头修建上游水库.电站的年发电量约为10亿kW•h,年抽水用电量约为14亿kW•h.如图所示,上游水库近似视为长方体,可用于发电的库容量为V,蓄水后上游水库的平均水深为d,蓄水后水位高出下游水面高度为H.已知下游水库的库容量远大于上游水库的库容量.
十三陵抽水蓄能电站的工作原理是,在用电低谷时,电站利用电网多余电能把水抽到高出蓄水池中,到用电高峰时,再利用蓄水池中的水发电.电站利用十三陵水库为下游水库,在蟒山后上寺沟头修建上游水库.电站的年发电量约为10亿kW•h,年抽水用电量约为14亿kW•h.如图所示,上游水库近似视为长方体,可用于发电的库容量为V,蓄水后上游水库的平均水深为d,蓄水后水位高出下游水面高度为H.已知下游水库的库容量远大于上游水库的库容量.