Question

【题目】(16分)如图所示，内壁光滑的半径为R的圆形轨道，固定在竖直平面内，质量为m1小球静止在轨道最低点，另一质量为m2的小球（两小球均可视为质点）从内壁上与圆心O等高的位置由静止释放，到最低点时与m1发生弹性碰撞，求：

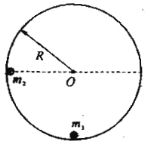
（1）小球m2运动到最低点时的速度大小；

（2）碰撞后，欲使m1能沿内壁运动到最高点，则m2/m1应满足什么条件？

Answer 1

【答案】（1）；（2）

【解析】（1）设小球m2运动到最低点时的速度为v0，由机械能守恒，得

①

解得 ②

（2）设弹性碰撞后，m1、m2两球的速度分别为v1、v2，则

③

④

由③④两式解得 ⑤（另一解不合实际，舍去）

设m1运动到轨道的最高点时速度为v，则有

⑥

小球m1由最低点运动最高点的过程中机械能守恒，则

⑦

由②⑤⑥⑦式解得 ⑧

根据机械能守恒求解出最低速度；再根据动量守恒求出碰后的速度，然后根据圆周运动的临界问题及机械能守恒求解。