题目内容
7.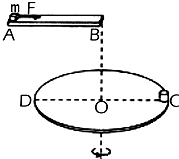 如图所示,水平放置的圆盘半径为R=1m,在其边缘C点固定一个高度不计的小桶,在圆盘直径CD的正上方放置一条水平滑道AB,滑道与CD平行.滑道右端B与圆盘圆心O在同一竖直线上,其高度差为h=1.25m.在滑道左端静止放置质量为m=0.4kg的物块(可视为质点),物体与滑道间的动摩擦因数为μ=0.2.当用一大小为F=4N的水平向右拉力拉动物块的同时,圆盘从图示位置以角速度ω=2πrad/s,绕穿过圆心O的竖直轴匀速转动,拉力作用一段时间后撤掉,物块在滑道上继续滑行,由B点水平抛出,恰好落入小桶内,重力加速度取10m/s2.
如图所示,水平放置的圆盘半径为R=1m,在其边缘C点固定一个高度不计的小桶,在圆盘直径CD的正上方放置一条水平滑道AB,滑道与CD平行.滑道右端B与圆盘圆心O在同一竖直线上,其高度差为h=1.25m.在滑道左端静止放置质量为m=0.4kg的物块(可视为质点),物体与滑道间的动摩擦因数为μ=0.2.当用一大小为F=4N的水平向右拉力拉动物块的同时,圆盘从图示位置以角速度ω=2πrad/s,绕穿过圆心O的竖直轴匀速转动,拉力作用一段时间后撤掉,物块在滑道上继续滑行,由B点水平抛出,恰好落入小桶内,重力加速度取10m/s2.(1)若拉力作用时间为0.5s,求所需滑道的长度;
(2)求拉力作用时间满足什么条件?
分析 (1)物块离开B点后做平抛运动,可以求出平抛运动的时间和平抛运动的初速度,物块在滑道上先匀加速运动再匀减速运动,两个运动的位移之和为滑道的长度.
(2)抓住物块滑行时间、抛出在空中时间与圆盘周期关系:t1+t2+t=nT(n=1、2、3…),求出拉力作用时间满足的条件.
解答 解:(1)物块平抛,竖直方向上有:h=$\frac{1}{2}g{t}^{2}$,
解得:t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×1.25}{10}}s=0.5s$.
物块离开滑道时的速度为:v=$\frac{R}{t}=\frac{1}{0.5}m/s=2m/s$.
拉动物块的加速度,由牛顿第二定律:F-μmg=ma1;
代入数据解得:a1=8m/s2
撤去外力后,由牛顿第二定律:-μmg=ma2;
代入数据解得:a2=-2m/s2
匀加速运动的位移为:${x}_{1}=\frac{1}{2}{a}_{1}{{t}_{1}}^{2}$=$\frac{1}{2}$×8×0.25m=1m
匀加速运动的速度为:v1=a1t1=8×0.5m/s=4m/s,
匀减速运动的位移为:${x}_{2}=\frac{{v}^{2}-{{v}_{1}}^{2}}{2{a}_{2}}=\frac{4-16}{-4}m=3m$,
板长L=x1+x2=4m.故所需滑道的长度为4m.
(2)盘转过一圈时间:T=$\frac{2π}{ω}$=1s
设加速、减速时间分别为t1、t2,则物块在滑道上先加速后减速,最终获得:
v=a1t1-a2t2,
物块滑行时间、抛出在空中时间与圆盘周期关系:
t1+t2+t=nT(n=1、2、3…)
故拉力作用的时间为:${t}_{1}=(\frac{n}{5}+0.1)s$(n=1、2、3…)
答:(1)所需滑道的长度为4m.
(2)拉力作用时间满足${t}_{1}=(\frac{n}{5}+0.1)s$(n=1、2、3…)
点评 解决本题的关键知道物块整个过程的运动:匀加速直线运动、匀减速直线运动和平抛运动,知道三个过程的运动时间与圆盘转动的时间相等.以及熟练运用运动学公式.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
| A. | 沿x轴的正方向传播 | B. | 沿x轴的负方向传播 | ||
| C. | 波速为1m/s | D. | 波速为2.5m/s |
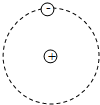 带负电量q的粒子绕固定的带正电Q的正电荷以速度v作顺时针方向的匀速圆周运动,粒子所在区间垂直圆周所在平面磁感应强度为B的匀强磁场,两电荷相距r,则( )
带负电量q的粒子绕固定的带正电Q的正电荷以速度v作顺时针方向的匀速圆周运动,粒子所在区间垂直圆周所在平面磁感应强度为B的匀强磁场,两电荷相距r,则( )| A. | 若Bqv<K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向里 | B. | 若Bqv<K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向外 | ||
| C. | 若Bqv>K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向里 | D. | 若Bqv>K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向外 |

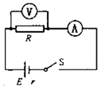 在如图所示的电路中,电源内电阻r=3Ω,当开关S闭合后电路正常工作,电压表的读数U=6V,电流表的读数I=1A.则电阻R=6Ω,电源电动势E=9V.
在如图所示的电路中,电源内电阻r=3Ω,当开关S闭合后电路正常工作,电压表的读数U=6V,电流表的读数I=1A.则电阻R=6Ω,电源电动势E=9V.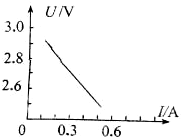 在《测量电源电动势和内电阻》的实验中,某同学得到的U-I图如图所示则电源电动势E=3.0V,内电阻r=1.0Ω,短路电流I源=3.0AA.
在《测量电源电动势和内电阻》的实验中,某同学得到的U-I图如图所示则电源电动势E=3.0V,内电阻r=1.0Ω,短路电流I源=3.0AA.