题目内容
18.甲、乙两列火车在同一轨道上同向行驶,甲车在前,其速度为v甲=10m/s,乙车在后,其速度为v乙=30m/s.因大雾能见度低,乙车在距甲车700m时才发现前方有甲车,这时乙车立即刹车,但要经过1800m乙车才能停下,且乙车在减速行驶20秒后开始鸣笛示警,甲车司机听到声音一秒后做出反应马上开始以a=0.25m/s2的加速度加速行驶.(已知声音传播的速度为335.125m/s;结果要求保留两位小数)试问:(1)甲车听到笛声时两车距离?
(2)两车能否相撞?若未相撞试求两车最近距离?
分析 (1)根据匀变速直线运动的速度位移公式v2-v02=2ax,求出乙车刹车的最大加速度,然后求出乙车在20s内的位移和此时两车之间的距离,由x=vt求出声音到达甲车的时间,然后由位移公式即可求出.
(2)在两车速度相等之前,两车的距离越来越小,若未相撞,则不会在相撞,因为速度相等之后,两车的距离又越来越大.所以在速度相等时,两车最近•
解答 解:(1)根据公式:v2-v02=2ax
乙车的加速度:a=$\frac{0-{v}_{乙}^{2}}{2x}=\frac{0-3{0}^{2}}{2×1800}=-0.25m/{s}^{2}$
乙车20s内的位移:${x}_{1}={v}_{乙}•{t}_{1}+\frac{1}{2}a{t}_{1}^{2}$=$30×20+\frac{1}{2}×(-0.25)×2{0}^{2}$=550m
乙的速度:v′=v乙+at1=30+(-0.25)×20=25m/s
甲的位移:x1′=v甲•t1=10×20=200m
此时甲与乙之间的距离:△x1=L+x1′-x1=700+200-550=350m
设甲车听到笛声时声波传播的时间是t2,则:(vs-v甲)t2=△x1
代入数据得:t2=1.0765s
此过程中甲的位移:x2′=v甲t2
乙的位移:x2=$v′{t}_{2}+\frac{1}{2}a{t}_{2}^{2}$
甲车听到笛声时两车距离:△x2=△x1+x2′-x1′
代入数据,联立得:△x2=334.00m
(2)当两车的速度相等时,v′+a(t2+1+t3)=v甲+a′t3
代入数据得:t3=47.347s
此过程中甲的位移:${x}_{3}′={v}_{甲}{t}_{3}+\frac{1}{2}a{′t}^{3}$=$10×47.347+\frac{1}{2}×0.25×47.34{7}^{2}=753.687$m
乙的位移:${x}_{3}=v′{t}_{3}+\frac{1}{2}a{t}^{3}$=$25×47.347+\frac{1}{2}×(-0.25)×47.34{7}^{2}=903.458$m
此时甲与乙之间的距离:△x3=△x1+x3′-x3=350+753.687-903.458=200.23m
所以两车不会相撞.
答:(1)甲车听到笛声时两车距离是334.00m
(2)两车不会相撞.若未相撞试求两车最近距离是200.23m
点评 解决本题的关键知道速度大者减速追速度小者,在速度相等之前,两车的距离越来越小,若未相撞,速度相等之后,两车的距离越来越大,可知只能在速度相等之时或相等之前相撞.

 精英口算卡系列答案
精英口算卡系列答案| A. | 牛顿发现了行星的运动规律 | |
| B. | 开普勒发现了万有引力定律 | |
| C. | 卡文迪许第一次在实验室里测出了万有引力常量 | |
| D. | 经典力学的适用范围是宏观世界,高速运动 |
| A. | 计算“和谐号”通过珠江的时间 | |
| B. | 对体操运动员姿势和动作进行分析 | |
| C. | “天宫一号”和“神舟八号”实现交会对接 | |
| D. | 研究“神舟八号”围绕地球做圆周运动的轨道半径 |
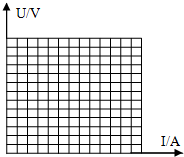 下面是在测某电源电动势和内阻的实验中纪录的六组数据.请在如图直角坐标系中画出U-I图象,待测电池的电动势为1.46V,内阻为0.84Ω.
下面是在测某电源电动势和内阻的实验中纪录的六组数据.请在如图直角坐标系中画出U-I图象,待测电池的电动势为1.46V,内阻为0.84Ω.| I/A | 0.10 | 0.15 | 0.25 | 0.37 | 0.40 | 0.50 |
| U/V | 1.38 | 1.34 | 1.25 | 1.15 | 1.20 | 1.05 |
A、转动选择开关置于“×1k”挡
B、转动选择开关置于“×100”挡
C、转动选择开关置于“×10”挡
D、转动选择开关置于“×1”挡
E、转动选择开关置于“OFF”挡
F、将两表笔分别接在R1两端,读出R1的值后断开
G、将两表笔分别接在R2两端,读出R2的值后断开
H、将两表笔短接,调节调零旋扭,使指针指在刻度线右端.
 如图所示,两个完全相同的小球A、B,在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出,下列说法正确的是( )
如图所示,两个完全相同的小球A、B,在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出,下列说法正确的是( )| A. | 从开始运动至落地,重力对两小球做功相同 | |
| B. | 从开始运动至落地,重力对两小球做功的平均功率相同 | |
| C. | 两小球落地时的速度相同 | |
| D. | 两小球落地时,重力的瞬时功率相同 |

| A. | 加5V电压时,灯泡的电阻小于5Ω | |
| B. | 加12V电压时,灯泡的电阻大于8Ω | |
| C. | 将两盏这种灯泡并联加12V电压时,每盏灯泡的功率小于18W | |
| D. | 由图可知,加5V电压时,灯泡的功率是5W |
| A. | 5J | B. | 20J | C. | 80J | D. | 125J |
| A. | ${\;}_{2}^{3}$He的原子核内有三个中子和两个质子 | |
| B. | ${\;}_{2}^{3}$He的原子核内有一个中子和两个质子 | |
| C. | ${\;}_{2}^{3}$He发生核聚变,放出能量,一定会有质量亏损 | |
| D. | ${\;}_{2}^{3}$He原子核内的核子靠万有引力紧密结合在一起 | |
| E. | ${\;}_{2}^{3}$He原子核与氘核聚变成${\;}_{2}^{4}$He的方程为:${\;}_{2}^{3}$He+${\;}_{1}^{2}$H→${\;}_{2}^{4}$He+${\;}_{1}^{1}$ H |
 如图所示,两颗绕地球作匀速圆周运动的卫星A、B分别距地高R、2R,两卫星轨道在同一平面内,且两卫星均沿顺时针方向运动,已知地球半径为R,地球表面重力加速度为g,求:
如图所示,两颗绕地球作匀速圆周运动的卫星A、B分别距地高R、2R,两卫星轨道在同一平面内,且两卫星均沿顺时针方向运动,已知地球半径为R,地球表面重力加速度为g,求: