题目内容
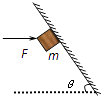
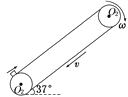
【题目】(10分)如图所示,与水平方向成37°角的传送带以恒定速度v=2 m/s沿顺时针方向转动,两传动轮间距L=5 m。现将质量为1 kg且可视为质点的物块以v0=4 m/s的速度沿传送带向上的方向自底端滑上传送带。物块与传送带间的动摩擦因数为μ=0.5,取g=10 m/s2,已知sin 37°=0.6,cos 37°=0.8,计算时,可认为滑动摩擦力近似等于最大静摩擦力,求物块在传送带上上升的最大高度。
【答案】0.96 m
【解析】物块刚滑上传送带时,物块相对传送带向上运动,受到摩擦力沿传送带向下,将匀减速上滑,直至与传送带等速,由牛顿第二定律得物块向上减速时有,物体上滑是的加速度为a1:
mgsinθ+μmgcosθ=ma1
则有:a1=g(sinθ+μcosθ)=10×(0.6+0.5×0.8)m/s2=10m/s2
物体沿传送带向上的位移为: ![]()
物块与传送带相对静止瞬间,由于最大静摩擦力f=μmgcosθ<mgsinθ,相对静止状态不能持续,物块速度会继续减小.此后,物块受到滑动摩擦力沿传送带向上,但合力沿传送带向下,故继续匀减速上升,直至速度为零.令此时物体减速上升的加速度为a2则:
根据牛顿第二定律可得:mgsinθ-μmgcosθ=ma2
得:a2=g(sinθ-μcosθ)=10×(0.6-0.5×0.8)m/s2=2m/s2
物体沿传送带向上运动的位移为: ![]()
则物块沿传送带上升的最大高度为:H=(x1+x2)sin37°=(0.6+1)×0.6m=0.96m

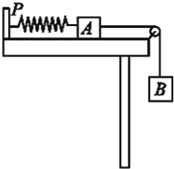
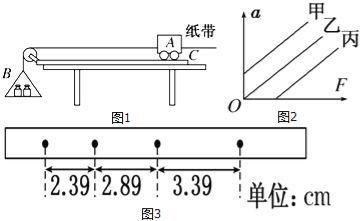
【题目】如图1所示,为“探究加速度与力、质量的关系”实验装置图.图1中A为小车,B为砝码及砝码盘,C为一端带有定滑轮的长木板,小车通过纸带与打点计时器相连,计时器接50Hz交流电.小车A的质量为m1,砝码及砝码盘B的质量为m2.
(1)下列说法正确的是 .
A.每次改变小车质量时,应重新平衡摩擦力 |
B.实验时应先释放小车后接通电源 |
C.本实验m2应远大于m1 |
D.在用图象探究加速度与质量关系时,应作a﹣ |
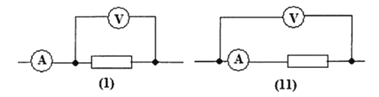
(2)实验时,某同学由于疏忽,遗漏了平衡摩擦力这一步骤,他测量得到的a﹣F图象,可能是图2中的图线 .(选填“甲”“乙”或“丙”)
(3)如图3所示为某次实验得到的纸带,纸带中相邻计数点间的距离已标出,相邻计数点间还有四个点没有画出.由此可求得小车的加速度大小为 m/s2.(结果保留两位有效数字)