题目内容
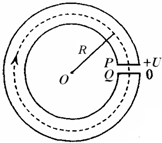 如图所示为一种获得高能粒子的装置--环形加速器.环形区域内存在垂直纸面向外的匀强磁场,磁场的磁感应强度大小可调节.质量为m、电量为+q的粒子可在环中做匀速圆周运动.P、Q为相距很近的两块中心开有小孔的极板,最初两极板电势都为零,每当粒子飞至P板时,P板电势变为+U,Q板电势仍保持为零,每当粒子离开Q板时,P板电势立即变为零.粒子在P、Q两板间电场的一次次加速下动能不断增大,而粒子的绕行半径通过磁场的调节保持为R不变.粒子经过P、Q极板的时间极短,可忽略不计.设t=0时刻,粒子静止在P板小孔处,在电场作用下加速,并绕行第一圈.
如图所示为一种获得高能粒子的装置--环形加速器.环形区域内存在垂直纸面向外的匀强磁场,磁场的磁感应强度大小可调节.质量为m、电量为+q的粒子可在环中做匀速圆周运动.P、Q为相距很近的两块中心开有小孔的极板,最初两极板电势都为零,每当粒子飞至P板时,P板电势变为+U,Q板电势仍保持为零,每当粒子离开Q板时,P板电势立即变为零.粒子在P、Q两板间电场的一次次加速下动能不断增大,而粒子的绕行半径通过磁场的调节保持为R不变.粒子经过P、Q极板的时间极短,可忽略不计.设t=0时刻,粒子静止在P板小孔处,在电场作用下加速,并绕行第一圈.(1)为使粒子始终在半径为R的圆轨道上运动,磁场必须周期性递增.求粒子从t=0时刻起绕行第n圈时的磁感应强度Bn;
(2)求粒子从t=0时刻起绕行n圈回到P板所需的总时间tn.
分析:(1)由电场力做导致粒子的动能增加,结合动能定理,可求出n圈后的速度,再根据牛顿第二定律与向心力公式,即可求解;
(2)根据第n圈所需时间,结合数学通项式,即可求解.
(2)根据第n圈所需时间,结合数学通项式,即可求解.
解答:解:(1)粒子绕行n圈获得的动能等于电场力对粒子做的功,设粒子绕行n圈获得的速度为vn,
根据动能定理,
则有:nqU=
m
解得:vn=
粒子在环形区域磁场中,受洛伦兹力作用做半径为R的匀速圆周运动,
根据牛顿第二定律和向心力公式,
则有:qvnBn=m
解得:Bn=
=
(2)粒子绕行第n圈所需时间Tn=
=2πR
?
粒子绕行n圈所需总时间为tn=2πR
(1+
+
+…+
).
答:(1)粒子从t=0时刻起绕行第n圈时的磁感应强度得:Bn=
=
;
(2)粒子从t=0时刻起绕行n圈回到P板所需的总时间为tn=2πR
(1+
+
+…+
).
根据动能定理,
则有:nqU=
| 1 |
| 2 |
| v | 2 n |
解得:vn=
|
粒子在环形区域磁场中,受洛伦兹力作用做半径为R的匀速圆周运动,
根据牛顿第二定律和向心力公式,
则有:qvnBn=m
| ||
| R |
解得:Bn=
| mvn |
| qR |
| 1 |
| R |
|
(2)粒子绕行第n圈所需时间Tn=
| 2πR |
| vn |
|
| 1 | ||
|
粒子绕行n圈所需总时间为tn=2πR
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
答:(1)粒子从t=0时刻起绕行第n圈时的磁感应强度得:Bn=
| mvn |
| qR |
| 1 |
| R |
|
(2)粒子从t=0时刻起绕行n圈回到P板所需的总时间为tn=2πR
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
点评:考查粒子在电场力作用下,电场力做功从而获得动能,掌握动能定理、牛顿第二定律与向心力公式的应用,掌握粒子做匀速圆周运动的周期公式,及运用数学的通项式.

练习册系列答案
相关题目
 美国物理学家劳伦斯于1932年发明的回旋加速器,应用带电粒子在磁场中做圆周运动的特点,能使粒子在较小的空间范围内经过电场的多次加速获得较大的能量,使人类在获得以较高能量带电粒子方面前进了一步,如图所示为一种改进后的回旋加速器示意图,其中盒缝间的加速电场场强大小恒定,且被限制在A、C板间,带电粒子从P0处静止释放,并沿电场线方向射入加速电场,经加速后再进入D形盒中的匀强磁场做匀速圆周运动,盒缝间隙很小,可以忽略不计.对于这种改进后的回旋加速器,下列说法正确的是( )
美国物理学家劳伦斯于1932年发明的回旋加速器,应用带电粒子在磁场中做圆周运动的特点,能使粒子在较小的空间范围内经过电场的多次加速获得较大的能量,使人类在获得以较高能量带电粒子方面前进了一步,如图所示为一种改进后的回旋加速器示意图,其中盒缝间的加速电场场强大小恒定,且被限制在A、C板间,带电粒子从P0处静止释放,并沿电场线方向射入加速电场,经加速后再进入D形盒中的匀强磁场做匀速圆周运动,盒缝间隙很小,可以忽略不计.对于这种改进后的回旋加速器,下列说法正确的是( )

