题目内容
如图,一个倾角为45°的斜面固定于竖直墙上,为使一光滑的均质铁球静止在如图所示的位置,需用一个水平推力F作用于球体上,F的作用线通过球心.设球体的重力为G,竖直墙对球体的弹力为N1,斜面对球体的弹力为N2,则下列正确的是( )
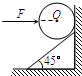
| A.N1=F | B.G≤F |
| C.N2>G | D.N2一定大于N1 |

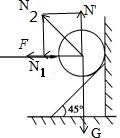
如图所示,小球受重力、推力、斜面的支持力及竖直墙的支持力;将斜面的支持力进行分解为竖直方向上的N′=N2cos45°、水平向上的N″=N2sin45°,则由共点力的平衡条件可知:水平方向上:F=N1+N″=N1+N2sin45°;故F一定大于N1;故A错误;
竖直方向上:G=N′=N2cos45°
故N2=
G,故N2>G,故C正确;
联立两式可得:G=F-N1;故G<F;
若压力F等于N2水平向上的分力时,小球有可能对竖直面没有压力,故N1有可能为零,故G可以等于F;
故G≤F,故B正确;
由以上分析可知,物体的平衡关系无法判断N1、N2的大小关系,故D错误;
故选B、C.
竖直方向上:G=N′=N2cos45°
故N2=
| 2 |
联立两式可得:G=F-N1;故G<F;
若压力F等于N2水平向上的分力时,小球有可能对竖直面没有压力,故N1有可能为零,故G可以等于F;
故G≤F,故B正确;
由以上分析可知,物体的平衡关系无法判断N1、N2的大小关系,故D错误;
故选B、C.


练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
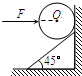 (2011?黄浦区一模)如图,一个倾角为45°的斜面固定于竖直墙上,为使一光滑的均质铁球静止在如图所示的位置,需用一个水平推力F作用于球体上,F的作用线通过球心.设球体的重力为G,竖直墙对球体的弹力为N1,斜面对球体的弹力为N2,则下列正确的是( )
(2011?黄浦区一模)如图,一个倾角为45°的斜面固定于竖直墙上,为使一光滑的均质铁球静止在如图所示的位置,需用一个水平推力F作用于球体上,F的作用线通过球心.设球体的重力为G,竖直墙对球体的弹力为N1,斜面对球体的弹力为N2,则下列正确的是( )
 如图,一个倾角为45°的斜面固定于竖直墙上,为使一光滑的均质铁球静止在如图所示的位置,需用一个水平推力F作用于球体上,F的作用线通过球心.设球体的重力为G,竖直墙对球体的弹力为N1,斜面对球体的弹力为N2,则下列正确的是( )
如图,一个倾角为45°的斜面固定于竖直墙上,为使一光滑的均质铁球静止在如图所示的位置,需用一个水平推力F作用于球体上,F的作用线通过球心.设球体的重力为G,竖直墙对球体的弹力为N1,斜面对球体的弹力为N2,则下列正确的是( )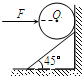 如图,一个倾角为45°的斜面固定于竖直墙上,为使一光滑的均质铁球静止在如图所示的位置,需用一个水平推力F作用于球体上,F的作用线通过球心.设球体的重力为G,竖直墙对球体的弹力为N1,斜面对球体的弹力为N2,则下列正确的是( )
如图,一个倾角为45°的斜面固定于竖直墙上,为使一光滑的均质铁球静止在如图所示的位置,需用一个水平推力F作用于球体上,F的作用线通过球心.设球体的重力为G,竖直墙对球体的弹力为N1,斜面对球体的弹力为N2,则下列正确的是( )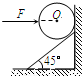 如图,一个倾角为45°的斜面固定于竖直墙上,为使一光滑的均质铁球静止在如图所示的位置,需用一个水平推力F作用于球体上,F的作用线通过球心.设球体的重力为G,竖直墙对球体的弹力为N1,斜面对球体的弹力为N2,则下列正确的是( )
如图,一个倾角为45°的斜面固定于竖直墙上,为使一光滑的均质铁球静止在如图所示的位置,需用一个水平推力F作用于球体上,F的作用线通过球心.设球体的重力为G,竖直墙对球体的弹力为N1,斜面对球体的弹力为N2,则下列正确的是( )