Question

【题目】如图所示，一质量为m=1．5kg的滑块从倾角为θ=37°的斜面上自静止开始滑下，斜面末端水平（水平部分光滑，且与斜面平滑连接，滑块滑过斜面末端时无能量损失），滑块离开斜面后水平滑上与平台等高的小车．已知斜面长s=10m，小车质量为M=3．5kg，滑块与斜面及小车表面的动摩擦因数μ=0．35，小车与地面光滑且足够长，取g=10m/s2．

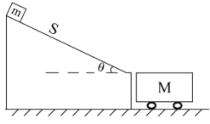
求：（1）滑块滑到斜面末端时的速度

（2）当滑块与小车相对静止时，滑块在车上滑行的距离

Answer 1

【答案】（1）8 m/s（2）6．4m

【解析】

试题分析：（1）设滑块在斜面上的滑行加速度a，

由牛顿第二定律，有 mg（sinθ-μcosθ）=ma

代入数据得：a=3．2m/s2

又：s=at2

解得 t=2．5s

到达斜面末端的速度大小 v0=at=8 m/s

（2）小车与滑块达到共同速度时小车开始匀速运动，该过程中小车与滑块组成的系统在水平方向的动量守恒，则：mv0=（m+M）v

代入数据得：v=2．4m/s

滑块在小车上运动的过程中，系统减小的机械能转化为内能，得：

μmgL＝mv02（m+M）v2

代入数据得：L=6．4m