题目内容
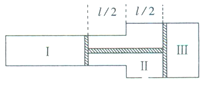
【题目】横截面积为S和2S的两圆柱形容器按图示方式连接成一气缸，每个圆筒中各置有一活塞，两活塞间的距离为l，用硬杆相连，形成“工”字形活塞，它把整个气缸分隔成三个气室，其中I、Ⅲ室密闭摩尔数分别为ν和2ν的同种理想气体，两个气室内都有电加热器；Ⅱ室的缸壁上开有一小孔，与大气相通；1 mol该种气体内能为CT(C是气体摩尔热容量，T是气体的绝对温度)。当三个气室中气体的温度均为T1时，“工"字形活塞在气缸中恰好在图所示的位置处于平衡状态，这时I室内气柱长亦为l，Ⅱ室内空气的摩尔数为
。已知大气压不变，气缸壁和活塞都是绝热的，不计活塞与气缸之间的摩擦。现通过电热器对I、Ⅲ两室中的气体缓慢加热，直至I室内气体的温度升为其初始状态温度的2倍时，活塞左移距离d，已知理想气体常量为R。求：
（1）Ⅲ室内气体初态气柱的长度；
（2）Ⅲ室内气体末态的温度；
（3）此过程中I、Ⅲ室密闭气体吸收的总热量。
【答案】（1）
（2）
（3）
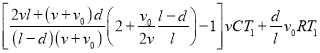
【解析】
（1）设大气压强为p0．初态：I室内气体压强为p1；III室内气体压强为p3，气柱的长度为l3；末态：I室内气体压强为p1′；III室内气体压强为p3′；由初态到末态：活塞左移距离为d。
首先用整体法，力学平衡
p3(2S)= p1S+ p0(2S－S)
然后对三部分气体分别
p1lS=νRT1
p0（
）
p3l3(2S)=(2ν)RT1
联立上述各式得：
=
得：
l3=
（2）方法同第（1）小题
p3′(2S)= p1′S+ p0(2S－S)
对I室中气体
p1′(l－d)S=νRT2=νR2T1
对III室中气体：
p3′(l3+d)(2S)=(2ν)RT3′
T3′=
（3）大气对密闭气体系统做的功为：
W=p0(2S－S)(－d)=－p0Sd=－
系统密闭气体内能增加量为
ΔU=νC(T1′－T1)+ (2ν)C(T3′－T3)
且初态T3= T1，故
ΔU=νC(2T3′－T1)
将T3′代去得
ΔU=[
－1]νCT1
密闭气体系统吸收的热量为
Q=ΔU－W=[－1]νCT1+
