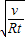题目内容
某人站在某一星球上，以速度v0竖直上抛一物体，经t 物体落回手中．已知该星球半径为R，现将此物体沿此行星表面抛出，欲使其不再落回到星球上，则抛出时速度至少为?（ ）
分析：由竖直上抛运动规律可求得该星球的重力加速度；若要使物体不再落后星球，应使物体绕着星球表面做匀速圆周运动，由万有引力定律充当向心力可求得抛出速度．
解答：解：物体向上和向下的时间相等，均为
，则由速度公式可得：
v0=g
；
解得：g=
；
在星球表面
要使物体不落后星球，则有：
G
=m
=mg=m
；
解得v=
故选B．
| t |
| 2 |
v0=g
| t |
| 2 |
解得：g=
| 2v0 |
| t |
在星球表面
要使物体不落后星球，则有：
G
| Mm |
| R2 |
| v2 |
| R |
| 2v0 |
| t |
解得v=
|
故选B．
点评：本题中要明确使小球不再回到星球表面是指使小球获得一定的速度而绕着星球表面做匀速圆周运动．
练习册系列答案
阅读快车系列答案
相关题目
?
?
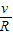
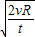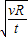