Question

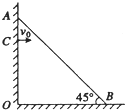
抛体运动在各类体育运动项目中很常见，如乒乓球运动．现讨论乒乓球发球问题，设球台长2L、网高h，乒乓球反弹前后水平分速度不变，竖直分速度大小不变、方向相反，且不考虑乒乓球的旋转和空气阻力．（设重力加速度为g）
（1）若球在球台边缘O点正上方高度为h₁处以速度v₁水平发出，落在球台的P₁（如图实线所示），求P₁点距O点的距离s₁；
（2）若球在O点正上方以速度v₂水平发出，恰好在最高点时越过球网落在球台的P₂点（如图虚线所示），求v₂的大小；
（3）若球在O点正上方水平发出后，球经反弹恰好越过球网且刚好落在对方球台边缘P₃处，求发球点距O点的高度h₃．

Answer 1

（1）设发球时飞行时间为t₁，根据平抛运动有：h1=

1

2

gt12
s₁=v₁t₁
解得：s₁=v1

2h1 g

．
（2）设发球高度为h₂，飞行时间为t₂，同理有：
h2=

1

2

gt22
x₂=v₂t₂
且h₂=h
2x₂=L
得：v2=

L

2

g 2h

．
（3）设球从恰好越过球网到最高点的时间为t，水平距离为s，根据抛体运动的特点及反弹的对称性，知反弹到最高点的水平位移为

2

3

L，
则反弹到越过球网的水平位移为L-

2

3

L=

1

3

L．在水平方向上做匀速直线运动，所以从越过球网到最高点所用的时间和从反弹到最高点的时间比为1：2．
对反弹到最高点的运动采取逆向思维，根据水平方向上的运动和竖直方向上的运动具有等时性，知越过球网到最高点竖直方向上的时间和反弹到最高点在竖直方向上的
时间比为1：2．
根据：h=

1

2

gt2得知越过球网到最高点竖直方向上的位移和反弹到最高点的位移为1：4，即：

h3-h

h3

=

1

4

解得：h3=

4

3

h．
答：（1）P₁点距O点的距离为v1

2h1 g

．
（2）v₂的大小为

L

2

g 2h

．
（3）发球点距O点的高度

4

3

h．