题目内容
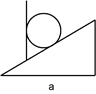
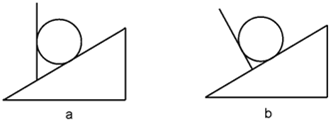
如图a所示,在倾角为α=37°的斜面上有一块竖直放置的档板,在档板和斜面之间放一个重力G=20N的光滑球,求:
(1)图a中小球受到挡板和斜面对它的弹力分别是多少?
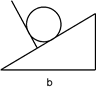
(2)若挡板是垂直斜面放置的,如图b所示,则挡板和斜面对小球的弹力又分别是多少?(sin37°=0.6,cos37°=0.8)
(1)图a中小球受到挡板和斜面对它的弹力分别是多少?
(2)若挡板是垂直斜面放置的,如图b所示,则挡板和斜面对小球的弹力又分别是多少?(sin37°=0.6,cos37°=0.8)

分析:(1)分析小球受力,画出受力图,根据平衡条件可知挡板和斜面对小球的弹力的合力与重力大小相等、方向相反,列式求解挡板和斜面对它的弹力.
(2)用同样的方法,求解挡板和斜面对它的弹力.
(2)用同样的方法,求解挡板和斜面对它的弹力.
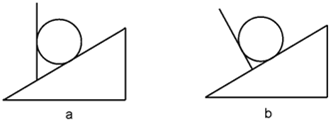
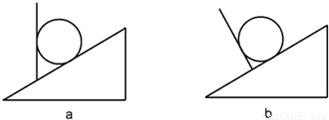
解答:解:根据图a所示,a球受到重力G、挡板的弹力F和斜面的弹力N,由平衡条件得知:N与F的合力与G大小相等、方向相反,如图,则有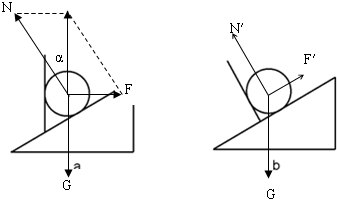
N=
=
N=25N
F=Gtan37°=20×0.75N=15N
根据图b所示,由平衡条件得
N′=Gcos37°=20×0.8N=16N
F′=Gsin37°=20×0.6N=12N
答:(1)图a中小球受到挡板和斜面对它的弹力分别是15N和25N.
(2)如图b所示,挡板和斜面对小球的弹力分别是12N和16N.

N=
| G |
| cosα |
| 20 |
| 0.8 |
F=Gtan37°=20×0.75N=15N
根据图b所示,由平衡条件得
N′=Gcos37°=20×0.8N=16N
F′=Gsin37°=20×0.6N=12N
答:(1)图a中小球受到挡板和斜面对它的弹力分别是15N和25N.
(2)如图b所示,挡板和斜面对小球的弹力分别是12N和16N.
点评:本题是三力平衡问题,分析受力,画出力图是关键.

练习册系列答案
相关题目