题目内容
两小球以95 m长的细线相连.两球从同一地点自由下落,其中一球先下落1 s另一球才开始下落.问后一球下落几秒线才被拉直?
答案:9s
解析:
解析:
|
剖析:方法一:“线被拉直”指的是两球发生的相对位移大小等于线长,应将两球的运动联系起来解,设后一球下落时间为ts,则先下落小球运动时间为(t+1)s,根据位移关系有: 解得:t=9 s 方法二:若以后下落的球为参考系,当后下落的球出发时前一个球的运动速度为v0=gt=10 m/s. 以后两球速度发生相同的改变,即前一球相对后一球的速度始终为v0=10 m/s,此时线已被拉长:Δl= 线被拉直可看成前一球相对后一球做匀速直线运动发生了位移: s=l-Δl=95 m-5 m=90 m 所以t= 规律总结:解决双体或多体问题要善于寻找对象之间的运动联系.解决问题要会从不同的角度来进行研究,如本题变换参考系进行求解. |

练习册系列答案
相关题目
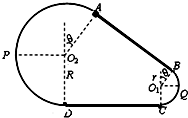 (2011?浙江模拟)如图所示为放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,其中倾斜直轨AB与水平直轨CD长均为L=3m,圆弧形轨道APD和BQC均光滑,BQC的半径为r=1m,APD的半径为R,AB、CD与两圆弧形轨道相切,O2A、O1B与竖直方向的夹角均为θ=370.现有一质量为m=1kg的小环穿在滑轨上,以某一初速度从B点开始沿AB向上运动,并恰能通过滑轨最高点.设小环与两段直轨道间的动摩擦因数均为
(2011?浙江模拟)如图所示为放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,其中倾斜直轨AB与水平直轨CD长均为L=3m,圆弧形轨道APD和BQC均光滑,BQC的半径为r=1m,APD的半径为R,AB、CD与两圆弧形轨道相切,O2A、O1B与竖直方向的夹角均为θ=370.现有一质量为m=1kg的小环穿在滑轨上,以某一初速度从B点开始沿AB向上运动,并恰能通过滑轨最高点.设小环与两段直轨道间的动摩擦因数均为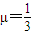 ,经过轨道连接
,经过轨道连接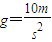 ,sin37°=0.6,cos37°=0.8,sin18.5°=0.32,cos18.5°=0.95,
,sin37°=0.6,cos37°=0.8,sin18.5°=0.32,cos18.5°=0.95,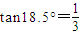 ,cot18.5°=3)求:
,cot18.5°=3)求: