Question

【题目】两个正点电荷Q1=Q和Q2=4Q分别置于固定在光滑绝缘水平面上的A、B两点，

（1）如图（a）所示，现将另一正电荷+q置于AB连线上靠近A处由静止释放。它将向B点运动，说明它从释放点到O点过程中速度和加速度的变化情况；

（2）接第一问现将另一正点电荷置于A、B连线上靠近A处静止释放，它在AB连线上运动过程中能达到最大速度的位置离A点的距离。

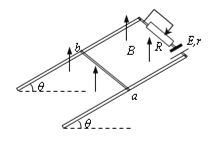
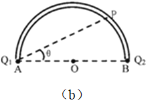
（3）如图（b）若把该点电荷放于绝缘管内靠近A点处由静止释放，试确定它在管内运动过程中速度为最大值时的位置P。即求出图中PA和AB连线的夹角θ。

Answer 1

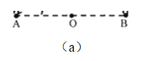
【答案】（1）速度先增加后减少，加速度先减小后增大；（2）；（3）arctan

【解析】

（1）将另一正电荷+q从A到B运动，由于AB的连线上电场方向先向右再向左，所以电场力先做正功后做负功，则动能先增加后减小；AB的连线上电场线先变疏后变密，所以电场强度先减小后增大，则电场力先减小后增大，根据牛顿第二定律，可知加速度先减小后增大；

（2）设在AB连线上运动过程中能达到最大速度的位置离A点的距离为x，正电荷在AB连线上速度最大处应该是电荷所受合力为零，即：

解得：

（3）若点电荷在P点处受到的库仑力的合力沿OP的方向，则它在P点处速度最大，即此时满足：

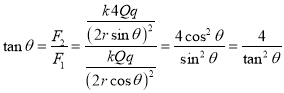
即：

解得：θ= arctan.