题目内容
3. 如图所示,边界OA与OC之间分布有垂直纸面向里的匀强磁场,磁感应强度为B,边界OC上有一荧光屏(粒子打在上面,可激发荧光),边界OA上距O点距离为L处有一粒子源S,从某一时刻起,从S平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒了间的相互作用力),所有粒子的初速度大小相同,经过一段时间后有大量粒子从边界OC射出磁场打在荧光屏上,已知∠AOC=60°,打在荧光屏上的粒子在磁场中运动的最短时间等于$\frac{T}{6}$(T为粒子在磁场中运动的周期,用T为已知值),求:
如图所示,边界OA与OC之间分布有垂直纸面向里的匀强磁场,磁感应强度为B,边界OC上有一荧光屏(粒子打在上面,可激发荧光),边界OA上距O点距离为L处有一粒子源S,从某一时刻起,从S平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒了间的相互作用力),所有粒子的初速度大小相同,经过一段时间后有大量粒子从边界OC射出磁场打在荧光屏上,已知∠AOC=60°,打在荧光屏上的粒子在磁场中运动的最短时间等于$\frac{T}{6}$(T为粒子在磁场中运动的周期,用T为已知值),求:(1)粒子的质量和电荷量的比值;
(2)粒子做圆周运动的半径;
(3)粒子打在荧光屏上形成的亮线的长度.
分析 (1)已知粒子在磁场中做圆周运动的周期,根据粒子周期公式可以求出粒子的质量和电荷量的比值;
(2)粒子在磁场中运动做匀速圆周运动,所有粒子的初速度大小相同,轨迹半径相同,弦越大,轨迹的圆心越大,运动时间越长.
(3)求出粒子打在OC上的最大与最小距离,然后确定范围.
解答 解:(1)粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,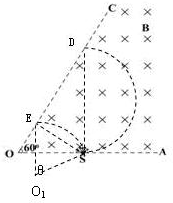
则粒子的质量和电荷量的比值为:$\frac{m}{q}$=$\frac{BT}{2π}$;
(2)粒子在磁场中运动做匀速圆周运动,入射点是S,出射点在OC直线上,出射点与S点的连线为轨迹的一条弦.
当从边界OC射出的粒子在磁场中运动的时间最短时,轨迹的弦最短,
根据几何知识,作ES⊥OC,则ES为最短的弦,粒子从S到E的时间即最短.
由题意可知,粒子运动的最短时间等于:$\frac{T}{6}$,运动时间:t=$\frac{θ}{360°}$T,解得:θ=60°,
设OS=L,则ES=$\frac{\sqrt{3}}{2}$L,由几何知识,得粒子运动的轨迹半径为R=ES=$\frac{\sqrt{3}}{2}$L;
(3)粒子打在OC上的最短距离:OE=$\frac{ES}{tan60°}$=$\frac{1}{2}$L,
当粒子轨迹的弦是直径时运动时间最长,打在OC上的距离最大,OD=$\frac{2R}{sin60°}$=2L,
粒子打在荧光屏上形成的亮线的长度:d=OD-0E=$\frac{3}{2}$L;
答:(1)粒子的质量和电荷量的比值为$\frac{BT}{2π}$;
(2)粒子做圆周运动的半径为$\frac{\sqrt{3}}{2}$L;
(3)粒子打在荧光屏上形成的亮线的长度为$\frac{3}{2}$L.
点评 本题考查了粒子在磁场中的运动,带电粒子在磁场中圆周运动的问题是高考的热点,也是难点,关键是运用几何知识画出轨迹.

| A. | $\frac{t}{4}$ | B. | $\frac{t}{2}$ | C. | 2t | D. | 4t |
| A. | 任意1秒内的速度变化2m/s | B. | 物体的加速度为6m/s2 | ||
| C. | 计时起点t=0时的速度为0 m/s | D. | 第1秒内的平均速度为6m/s |
| A. | 200 W | B. | 500 W | C. | 1 000 W | D. | 1 500 W |
| A. | 轻弹簧的劲度系数为$\frac{{F}_{2}-{F}_{1}}{{l}_{2}-{l}_{1}}$ | |
| B. | 轻弹簧的劲度系数为$\frac{{F}_{2}+{F}_{1}}{{l}_{2}-{l}_{1}}$ | |
| C. | 轻弹簧的原长为$\frac{{F}_{1}{l}_{2}+{F}_{2}{l}_{1}}{{F}_{1}+{F}_{2}}$ | |
| D. | 轻弹簧的原长为$\frac{{F}_{1}{l}_{2}-{F}_{2}{l}_{1}}{{F}_{1}-{F}_{2}}$ |
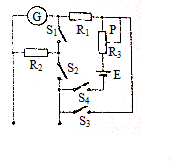 如图所示为一只三用表的电路原理图,则( )
如图所示为一只三用表的电路原理图,则( )| A. | 合上S1和S4时,可作电流表用 | B. | 只合上S2,可作电压表用 | ||
| C. | 只合上S2,可作欧姆表用 | D. | 只合上S3,可作电压表用 |
| A. | 一个物体在某一位置的重力势能是一个确定的值,与参考点的选择无关 | |
| B. | 一个物体从一个位置运动到另一个位置的过程中,重力势能的变化量与参考点的选择有关,选不同的参考点,重力势能的变化量不同 | |
| C. | 一个物体从一个位置运动到另一个位置的过程中,重力所做的功等于重力势能的减小量 | |
| D. | 用手把一个物体举高,手对物体所做的功等于物体重力势能的增加量 |