题目内容
【题目】质量为m电荷量为+q的带电粒子(不考虑重力)从半圆形区域边界A点沿直径方向正对圆心两次以相同速度v水平射入。第一次射入时,空间中只有竖直向下的匀强电场,第二次只有垂直于纸面向外的匀强磁场(磁场和电场区域都无限大且未画出)。发现带电粒子两次都击中半圆形边界上同一点B。
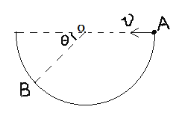
(1)证明两次粒子打到B点速度方向不同;
(2)判断两次粒子打到B点的时间长短,并加以证明。
【答案】(1)因为![]() ,所以两次粒子打到B点速度方向不同;(2)第一次粒子做平抛运动,沿直径方向的速度不变;第二次粒子做匀速圆周运动,沿直径方向的速度逐渐变小,而两次都击中半圆形边界上同一点B,两次沿直径方向的位移相等,所以第二次用时较长,证明见详解。
,所以两次粒子打到B点速度方向不同;(2)第一次粒子做平抛运动,沿直径方向的速度不变;第二次粒子做匀速圆周运动,沿直径方向的速度逐渐变小,而两次都击中半圆形边界上同一点B,两次沿直径方向的位移相等,所以第二次用时较长,证明见详解。
【解析】
(1)设半圆形区域的半径为r,B点与圆心连线和半圆形直径方向的夹角为![]() ,第一次射入时,带正电的粒子做类平抛运动,水平方向
,第一次射入时,带正电的粒子做类平抛运动,水平方向
r+r![]() =vt
=vt
竖直方向的速度
vy=![]() t=
t=![]()
第一次射出B点速度与直径方向的夹角
![]() =
=![]() =
=![]()
第二次射入时,粒子做匀速圆周运动,径向射入,径向射出,射出B点速度与直径方向的夹角为![]() ,做匀速圆周运动的半径
,做匀速圆周运动的半径
R=![]()
![]() =
=![]() =
=![]()
第二次射出B点速度与直径方向的夹角
![]() =
=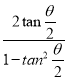 =
=![]()
因为![]() ,所以两次粒子打到B点速度方向不同。
,所以两次粒子打到B点速度方向不同。
(2)第一次粒子做平抛运动,沿直径方向的速度不变;第二次粒子做匀速圆周运动,沿直径方向的速度逐渐变小,而两次都击中半圆形边界上同一点B,两次沿直径方向的位移相等,所以第二次用时较长。
第一次在水平方向
r+r![]() =vt1
=vt1
第一次粒子在电场中运动的时间
t1=![]()
第二次粒子在磁场中运动的半径
R=![]() =
=![]()
qB=
第二次粒子在磁场中运动的
t2=![]() T=
T=![]() =
=![]() =
=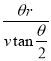 =
=![]()
因为![]() ,所以t2
,所以t2![]() t1。
t1。

练习册系列答案
相关题目