题目内容
某人在距离地面2.6m的高处,将质量为0.2Kg的小球以vo=12m/S速度斜向上抛出,小球的初速度方向与水平方向之间的夹角为30°,g取10m/S2,求
(1)人抛球时对球做多少功?
(2)若不计空气阻力,小球落地时的速度大小是多少?
(3)若小球落地时的速度大小为V1=13m/S,小球在空中运动过程中克服阻力做了多少功?
(1)人抛球时对球做多少功?
(2)若不计空气阻力,小球落地时的速度大小是多少?
(3)若小球落地时的速度大小为V1=13m/S,小球在空中运动过程中克服阻力做了多少功?
14.4J 14m/S 2.7J
试题分析:根据动能定理求出所做的功,利用机械能守恒定律进行求解落地速度。根据功能关系求出克服阻力做的功。
(1)在抛出小球的过程中,只有人对小球做功。初态为静止,末态小于离手时速度为
 ,根据动能定理
,根据动能定理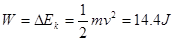
(2)在高处时的机械能:
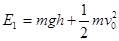
落地时的机械能:
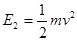
在空中运动的过程中,机械能守恒,即
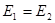 ,所以
,所以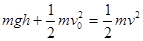
代入数据可求得 v=14m/s
(3)空气阻力对小球做的功等于小球机械能的变化
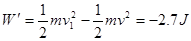
所以小球在空中运动的过程中,克服阻力所做的功
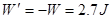
点评:本题难度减小,在求解物体机械能变化时应根据除了重力以外其它力做功判断

练习册系列答案
相关题目
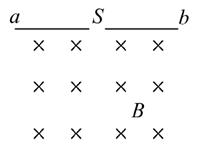
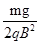
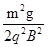
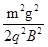

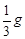 的加速度由静止竖直下落到地面,下列说法中正确的是( )
的加速度由静止竖直下落到地面,下列说法中正确的是( )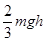
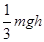
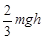
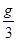 的加速度由静止竖直下落到地面。下列说法中正确的是( )
的加速度由静止竖直下落到地面。下列说法中正确的是( )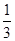 mgh
mgh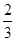 mgh
mgh