题目内容
 (2011?重庆)某行星和地球绕太阳公转的轨道均可视为圆.每过N年,该行星会运行到日地连线的延长线上,如图所示.该行星与地球的公转半径比为( )
(2011?重庆)某行星和地球绕太阳公转的轨道均可视为圆.每过N年,该行星会运行到日地连线的延长线上,如图所示.该行星与地球的公转半径比为( )分析:由图可知行星的轨道半径大,那么由开普勒第三定律知其周期长,其绕太阳转的慢.每过N年,该行星会运行到日地连线的延长线上,说明N年地球比行星多转1圈,即行星转了N-1圈,从而再次在日地连线的延长线上,那么,可以求出行星的周期是
年,接着再由开普勒第三定律求解该行星与地球的公转半径比.
| N |
| N-1 |
解答:解:A、B、C、D:由图可知行星的轨道半径大,那么由开普勒第三定律知其周期长.每过N年,该行星会运行到日地连线的延长线上,说明从最初在日地连线的延长线上开始,每一年地球都在行星的前面比行星多转圆周的N分之一,N年后地球转了N圈,比行星多转1圈,即行星转了N-1圈,从而再次在日地连线的延长线上.所以行星的周期是
年,根据开普勒第三定律有
=
,即:
=
=(
)
,所以,选项A、C、D错误,选项B正确.
故选:B.
| N |
| N-1 |
| ||
|
| ||
|
| r行 |
| r地 |
| 3 |
| ||||||
| N |
| N-1 |
| 2 |
| 3 |
故选:B.
点评:解答此题的关键由题意分析得出每过N年地球比行星多围绕太阳转一圈,由此求出行星的周期,再由开普勒第三定律求解即可.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
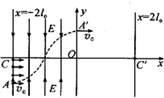 (2011?重庆模拟)如图所示的直角坐标系中,从直线x=-2l0到y轴区域存在两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界从A(-2l0,-l0)点到C(-2l0,0)点的区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起,A点到C点间的粒子依次连续以相同速度v0沿x轴正方向射入电场.从A点射入的粒子恰好从y轴上的A'(0,l0)点沿x轴正方向射出电场,其轨迹如图所示.不计粒子的重力及它们间的相互作用.
(2011?重庆模拟)如图所示的直角坐标系中,从直线x=-2l0到y轴区域存在两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界从A(-2l0,-l0)点到C(-2l0,0)点的区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起,A点到C点间的粒子依次连续以相同速度v0沿x轴正方向射入电场.从A点射入的粒子恰好从y轴上的A'(0,l0)点沿x轴正方向射出电场,其轨迹如图所示.不计粒子的重力及它们间的相互作用.
