题目内容
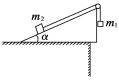
【题目】质量分别为m1和m2的两个小物块用轻绳连接,绳跨过位于倾角α=30°的光滑斜面顶端的轻滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上,如图所示.第一次,m1悬空,m2放在斜面上,用t表示m2自斜面底端由静止开始运动至斜面顶端所需的时间;第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上.如果![]() ,求m1自斜面底端由静止开始运动至斜面顶端所需的时间为多少?
,求m1自斜面底端由静止开始运动至斜面顶端所需的时间为多少?
【答案】![]()
【解析】
试题分析:第一次,设m2的加速度为a1,对m2,由牛顿第二定律有:FT-m2gsinα=m2a1
对m1,有:m1g-FT=m1a1
两式相加得: m1g-m2gsinα=(m1+m2)a1
设斜面长为l,则有:l=![]() a1t2
a1t2
第二次,设m1的加速度为a2,同理可得:m2g-m1gsinα=(m1+m2)a2
l=![]() a2t′2
a2t′2
又![]()
联立解得:![]()

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目