Question

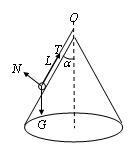
表面光滑的正圆锥体，母线与轴线间夹角α=37°，细线长L=

2

3

m，一端固定于圆锥顶点上的O点．当质量为m=1kg，的小球以速率v=

8

3

m/s绕圆锥轴线在水平面内作匀速圆周运动时，取g=10m/s²，求绳子的张力T．
某同学求解思路如下：
先进行受力分析，小球受到重力G、绳子拉力T和锥体的弹力N，画出受力图，如图所示．由于小球绕锥体在水平面内作圆周运动，所以将这三个力沿水平方向和竖直方向进行分解，得到下面二个方程　Tsinα-Ncosα=m

v2

Lsinα

　①
      Tcosα+Nsinα=mg　　　  ②
将α=37°、L=

2

3

m、m=1kg、v=

8

3

m/s代入上面二式，可求得绳子的张力T．
问该同学的解题思路是否正确？若正确求则出绳子张力T，若有错误请给出正确分析和解答．

Answer 1

分析：该同学没有分析小球是否离开圆锥体表面．当小球即将与圆锥体表面脱离时，取N=0，根据向心力公式求出此时的速度，跟题中的速度进行比较，然后再进行受力分析，根据向心力公式进行求解．

解答：解：不正确，
当小球即将与圆锥体表面脱离时，取N=0，
此时有mgtanα=m

v 2 c

Lsinα

，
代入数据可得vc=

3

m/s＜v=

8

3

m/s，
说明小球已脱离圆锥体表面，假设小球飘离后细线与轴线间的夹角为θ，
则有mgtanθ=m

v2

Lsinθ

，
代入数据得cosθ=

3

5

即θ=53°，
则T=

mg

cosθ

=

50

3

N
答：不正确，绳子张力T为

50

3

N

点评：本题的关键点在于判断小球是否离开圆锥体表面，不能直接应用向心力公式求解，难度适中．