题目内容
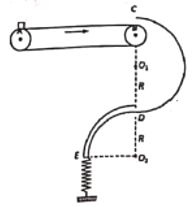
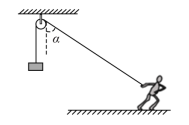
【题目】某玩具厂设计出如图所示的玩具,轨道固定在高为H1=0.5 m的水平台面上,通过在A处压缩弹簧把质量m=0.01 kg的小球(可看作质点)从静止弹出,先后经过直线轨道AC、半径R1=0.1 m的圆形轨道、长为L1=0.5 m 的直线轨道CD、以及两段半径R2=1 m的圆弧DE、GP,G、E两点等高且两圆弧对应的圆心角都为37°,所有轨道都平滑连接;小球从P点水平抛出后打到固定在Q点的锣上,P、Q的水平距离L2=1.2 m,锣的半径r= 0.3 m,圆心O离地高H2=0.4 m。CD段的动摩擦因数为0.2,其余轨道光滑,N为在P点正下方的挡板,在一次测试中测出小球运动到B点时对内轨的作用力为0.064 N。(sin 37°=0.6,cos 37°=0.8,g=10 m/s2)
(1)求小球运动到B点时的速度大小;
(2)小球能否离开轨道,请说明理由;
(3)要使小球打到锣上,求小球从A处弹出时弹簧对小球所做的功需满足的条件。

【答案】(1) v0=0.6 m/s (2)h0<2R1且h0<R2(1-cos37°),小球不离开轨道 (3) 0.1 J≤W≤0.23 J
【解析】
(1)由牛顿第二定律得
mg-FN=![]() ,
,
解得v0=0.6 m/s。
(2)设小球不离开轨道,通过直线轨道CD后能上升的最大高度为h0,则
mg(2R1-h0)-μmgL1=0-![]()
h0=0.118 m,h0<2R1且h0<R2(1-cos37°)
所以小球不离开轨道。
(3)锣的下边界与P点的高度差h1=0.8 m,上边界与P点的高度差h2=0.2 m,如果小球从P点飞出后能打到锣的上、下边界,根据平抛运动知识
![]()
v=![]()
可得从P点飞出的速度3 m/s≤v≤6 m/s,而小球沿圆弧GP运动到P点的条件
mg≤![]()
得v≥![]() m/s,所以
m/s,所以![]() m/s≤v≤6 m/s,根据动能定理得
m/s≤v≤6 m/s,根据动能定理得
W-μmgL1-mg[2R2(1-cos 37°)]=![]()
0.1 J≤W≤0.23 J。

 名校课堂系列答案
名校课堂系列答案