题目内容
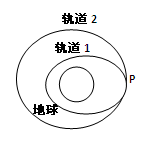
2010年10月1日“嫦娥二号”探月卫星沿地月转移轨道直奔月球,在距月球表面100km的P点进行第一次“刹车制动”后被月球捕获,进入椭圆轨道I绕月飞行,之后,卫星在P点又经过第二次“刹车制动”,进入距月球表面100km的圆形工作轨道II,绕月球做匀速圆周运动,如图所示。下列说法正确的是 ( )


| A.卫星在轨道I上经P点的速度等于卫星在轨道II上经过P点的速度 |
| B.卫星在轨道I上的机械能比在轨道II上大 |
| C.卫星在轨道I上运动周期比在轨道II上长 |
| D.卫星沿轨道I经P点时的加速度大于沿轨道II经P点时的加速度 |
BC
分析:根据开普勒第三定律的内容比较周期.
研究“嫦娥二号”绕月球做匀速圆周运动,根据万有引力提供向心力,列出等式表示出加速度的表达式.
通过两个轨道的位置关系进行比较.
解答:解:D、根据开普勒第三定律的内容:所有的行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
即:
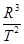 =K,K与中心体有关.
=K,K与中心体有关.通过题意我们知道:轨道Ⅰ的半长轴大于轨道Ⅰ的半径.
所以卫星在轨道Ⅰ上运动周期比在轨道Ⅱ上长,故B正确,A错误.
A、研究“嫦娥二号”绕月球做匀速圆周运动,根据万有引力提供向心力,列出等式:
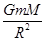 ="ma" 得出:a=
="ma" 得出:a= ,
,所以卫星沿轨道Ⅰ经P点时的加速度等于沿轨道Ⅱ经P点时的加速度.故D错误,C正确.
故选BC.
点评:要比较一个物理量大小,我们应该把这个物理量先表示出来,在进行比较.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

练习册系列答案
相关题目

 ~
~


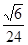
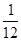
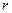 ,周期为
,周期为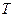 。月球质量为
。月球质量为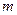 ,万有引力常量为G,求(1)地球对月球的万有引力为多大?(2)地球质量为多大?
,万有引力常量为G,求(1)地球对月球的万有引力为多大?(2)地球质量为多大?