题目内容
2. 如图所示,在光滑水平直导轨上,静止放着三个质量均为m=1kg的相同小球A、B、C.现让A球以v0=2m/s的速度向着B球运动,A、B两球碰撞后粘在一起,两球继续向右运动并跟C球碰撞,C球的最终速度vC=1m/s.则:
如图所示,在光滑水平直导轨上,静止放着三个质量均为m=1kg的相同小球A、B、C.现让A球以v0=2m/s的速度向着B球运动,A、B两球碰撞后粘在一起,两球继续向右运动并跟C球碰撞,C球的最终速度vC=1m/s.则:(1)A、B两球跟C球相碰前的共同速度为多大?
(2)A、B两球跟C球相碰后的共同速度为多大?
(3)两次碰撞过程中一共损失了多少动能?
分析 (1)A、B碰撞过程系统动力守恒,应用动量守恒定律可以求出碰撞后的速度;
(2)A、B、C系统动量守恒,应用动量守恒定律可以求出碰撞后的共同速度;
(3)对整个过程,应用能量守恒定律可以求出系统损失的动能.
解答 解:(1)A、B碰撞过程系统动量守恒,以A的初速度方向为正方向,由动量守恒定律得:
mv0=2mv1,
代入数据解得:v1=1m/s;
(2)A、B两球与C碰撞过程系统动量守恒,以A的初速度方向为正方向,由动量守恒定律得:
2mv1=mvC+2mv2,
代入数据解得:v2=0.5 m/s,
(3)由能量守恒定律得:△Ek=$\frac{1}{2}$mv02-$\frac{1}{2}$•2mv22-$\frac{1}{2}$mvC2,
代入数据解得:△Ek=1.25 J;
答:(1)A、B两球跟C球相碰前的共同速度为1m/s;
(2)A、B两球跟C球相碰后的共同速度为0.5m/s;
(3)两次碰撞过程中一共损失了1.25J的动能.
点评 本题考查了求速度、系统损失的动能,分析清楚物体运动过程、应用动量守恒定律与能量守恒定律即可正确解题.

练习册系列答案
相关题目
12.一质量为2kg的滑块,以4m/s的速度在光滑水平面上向左滑行.从某一时刻起,在滑块上作用一向右的水平力,经过一段时间,滑块的速度变为4m/s,方向水平向右.在这段时间里水平力做的功为( )
| A. | 0 | B. | 8 J | C. | 16 J | D. | 32 J |
13.下列情况下,物体的动量不变的是( )
| A. | 在平直路面上匀速前进的汽车? | |
| B. | 汽车在转弯的过程中 | |
| C. | 水平飞来的球撞到竖直墙面后又沿原路返回? | |
| D. | 匀速直线运动的洒水车正在洒水 |
10.关于质点做匀速圆周运动的下列说法正确的是( )
| A. | 由a=$\frac{{v}^{2}}{r}$ 知,a与r成反比 | B. | 由ω=2πn 知,ω与转速n成正比 | ||
| C. | 由ω=$\frac{v}{r}$ 知,ω与r成反比 | D. | 由a=ω2r 知,a与r成正比 |
17.关于质点做匀速圆周运动的下列说法正确的是( )
| A. | 由a=$\frac{{v}^{2}}{r}$知,a与r成反比 | B. | 由ω=$\frac{2π}{T}$知,ω与周期T成反比 | ||
| C. | 由a=ω2r知,a与r成正比 | D. | 由ω=$\frac{v}{r}$知,ω与r成反比 |
7.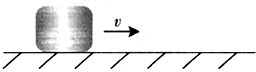 如图所示,质量为m的冰壶,与水平冰面间动摩擦因数为μ,被运动员以初速度v推出后,沿直线走了距离s后停止,下列说法中正确的有( )
如图所示,质量为m的冰壶,与水平冰面间动摩擦因数为μ,被运动员以初速度v推出后,沿直线走了距离s后停止,下列说法中正确的有( )
 如图所示,质量为m的冰壶,与水平冰面间动摩擦因数为μ,被运动员以初速度v推出后,沿直线走了距离s后停止,下列说法中正确的有( )
如图所示,质量为m的冰壶,与水平冰面间动摩擦因数为μ,被运动员以初速度v推出后,沿直线走了距离s后停止,下列说法中正确的有( )| A. | 摩擦力对冰壶做正功μmgs | B. | 冰壶克服摩擦力做功 | ||
| C. | 冰壶加速度大小为μg | D. | 合外力对冰壶做正功 |
14.如图所示,a、b、c是在地球大气层外圆形轨道上运行的三颗人造卫星.下列说法中正确的是( )


| A. | b、c的线速度大小相等,且大于a的线速度 | |
| B. | b、c的向心加速度大小相等,且小于a的向心加速度 | |
| C. | b、c运行周期相同,且小于a的运行周期 | |
| D. | b、c的角速度大小相等,且小于a的角速度 |
11.在平坦的垒球运动场上,击球手挥动球棒将垒球水平击出,垒球飞行一段时间后落地.若不计空气阻力,则( )
| A. | 垒球落地时瞬时速度的大小仅由初速度决定 | |
| B. | 垒球落地时瞬时速度的方向仅由击球点离地面的高度决定 | |
| C. | 垒球在空中运动的水平位移由初速度和高度共同决定 | |
| D. | 垒球在空中运动的时间仅由击球点离地面的高度决定 |
