Question

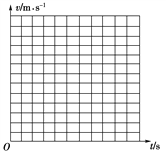
【题目】如图甲所示，一固定在地面上的足够长斜面，倾角为37°，物体A放在斜面底端挡板处，通过不可伸长的轻质绳跨过光滑轻质滑轮与物体B相连接，B的质量M＝1 kg，绳绷直时B离地面有一定高度．在t＝0时刻，无初速度释放B，由固定在A上的速度传感器得到的数据绘出的A沿斜面向上运动的v－t图象如图乙所示，若B落地后不反弹，g取10 m/s2，sin 37°＝0.6，cos 37°＝0.8.求：

(1)物体A与斜面间的动摩擦因数；

(2)物体A开始下滑的加速度大小．

Answer 1

【答案】(1)0.25　(2) 4m/s2

【解析】

由牛顿第二定律可得A受到的摩擦力，进而可得A与斜面的摩擦因数；AB具有相同的加速度，由此可得加速度。

(1)由图乙可知物体A先加速运动0.5 s，然后再匀减速运动0.25 s减速到零，加速度：

B落地后，由牛顿第二定律知：－mAgsinθ－μmAgcosθ＝mAa2

解得：μ＝0.25

(2)A下滑过程，由牛顿第二定律：mAgsinθ－μmAgcosθ＝mAa

代入数据得：a＝4 m/s2.